
分析 (1)由正弦定理可得AD=$\frac{CDsin∠ACD}{sin∠CAD}$≈101.2,即可求大楼的高度;
(2)tanα=tan(∠AME-∠BME)=$\frac{10x}{{x}^{2}+3224}$=$\frac{10}{x+\frac{3224}{x}}$≤$\frac{10}{4\sqrt{806}}$,即可得出结论.
解答 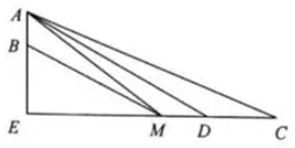 解:(1)由题意,∠ACD=31.80°,∠ADE=37.78°,
解:(1)由题意,∠ACD=31.80°,∠ADE=37.78°,
∠CAD=5.98°,CD=20,
由正弦定理可得AD=$\frac{CDsin∠ACD}{sin∠CAD}$≈101.2,
∴AE=ADsin∠ADE≈62m;
(2)设∠AMB=α,$α∈(0,\frac{π}{2})$,EM=x,x>0,
tan∠AME=$\frac{62}{x}$,tan∠AME=$\frac{52}{x}$,
tanα=tan(∠AME-∠BME)=$\frac{10x}{{x}^{2}+3224}$=$\frac{10}{x+\frac{3224}{x}}$≤$\frac{10}{4\sqrt{806}}$
当且仅当x=$\sqrt{3224}$≈57m时,tanα取得最大值,此时α也最大.
点评 本题考查正弦定理的运用,考查差角的正切公式,考查基本不等式的运用,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
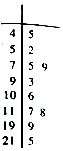 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为SO2、NO2、PM10、PM2.5、O3、CO等六项.空气质量按照AQI大小分为六级:一级0~50为优;二级51~100为良好;三级101~150为轻度污染;四级151~200为中度污染;五级201~300为重度污染;六级>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为SO2、NO2、PM10、PM2.5、O3、CO等六项.空气质量按照AQI大小分为六级:一级0~50为优;二级51~100为良好;三级101~150为轻度污染;四级151~200为中度污染;五级201~300为重度污染;六级>300为严重污染.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
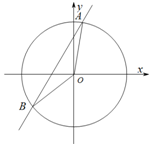 如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $-\frac{{\sqrt{5}}}{10}$ | C. | $\frac{9}{10}$ | D. | $-\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com