
定义域为[-1,1]的奇函数f(x)满足f(x)=f(x-2),且当x∈(0,1)时,f(x)=2x+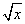 .
.
(1)求f(x)在[-1,1]上的解析式;
(2)求函数f(x)的值域.
解 (1)当x=0时,f(0)=-f(0),故f(0)=0.
当x∈(-1,0)时,-x∈(0,1),
f(x)=-f(-x)=-(-2x+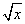 )=2x-
)=2x-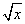 .
.
若x=-1时,f(-1)=-f(1).
又f(1)=f(1-2)=f(-1),故f(1)=-f(1),得f(1)=0,从而f(-1)=-f(1)=0.
综上,f(x)=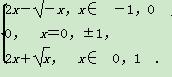
(2)∵x∈(0,1)时,f(x)=2x+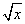 ,
,
∴f′(x)=2+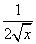 >0,故f(x)在(0,1)上单调递增.
>0,故f(x)在(0,1)上单调递增.
∴f(x)∈(0,3).
∵f(x)是定义域为[-1,1]上的奇函数,且f(0)=f(1)=f(-1)=0,
∴当x∈[-1,1]时,f(x)∈(-3,3).
∴f(x)的值域为(-3,3).


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
下列命题的否定为假命题的是( )
A.∃x0∈(-∞,0),使得2x0<3x0
B.任意一个四边形的四个顶点共圆
C.所有能被3整除的整数都是奇数
D.∀x∈R,sin2x+cos2x=1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=|x-2|+1,g(x)=kx.若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围是( )
A.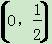 B.
B.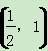
C.(1,2) D.(2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com