
分析 ①根据同角三角函数的关系消去参数θ得出曲线C的普通方程,即可得出曲线类型;
②写出曲线C′的参数方程,即P点坐标,求出直线l的普通方程.利用点到直线的距离公式得出距离d关于参数θ的函数,利用三角恒等变换及θ的范围得出d的最大值及P点坐标.
解答 解:①曲线C的普通方程为x2+(y-2)2=4,
曲线C表示圆心为(0,2),半径为2的圆.
②曲线C′的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ+1}\end{array}\right.$,∴P(2cosθ,sinθ+1),
直线l的普通方程为x+2y-12=0.
∴P到直线l的距离d=$\frac{|2cosθ+2sinθ+2-12|}{\sqrt{5}}$=$\frac{|2\sqrt{2}sin(θ+\frac{π}{4})-10|}{\sqrt{5}}$.
∴当sin($θ+\frac{π}{4}$)=-1即θ=$\frac{5π}{4}$时,d取得最大值$\frac{2\sqrt{2}+10}{\sqrt{5}}$=$\frac{2\sqrt{10}}{5}+2\sqrt{5}$.
此时,P点坐标为(-$\sqrt{2}$,1-$\frac{\sqrt{2}}{2}$).
点评 本题考查了参数方程与普通方程的转化,点到直线的距离公式及三角恒等变换,属于中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 32π | C. | 64π | D. | 128π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
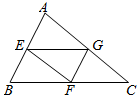 如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )
如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )| A. | 14π | B. | 15π | C. | $\frac{29}{2}$π | D. | 2$\sqrt{33}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 16π | C. | $\frac{16π}{3}$ | D. | $\frac{32π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com