Question

5．（1）函数y=log₂（x-1）的图象是由y=log₂x的图象如何变化得到的？
（2）在右边的坐标系中作出y=|log₂（x-1）|的图象．
（3）设函数y=${（\frac{1}{2}）}^{x}$与函数y=|log₂（x-1）|的图象的两个交点的横坐标分别为x₁，x₂，设M=x₁x₂-2（x₁+x₂）+4，请判断M的符号．

Answer 1

分析 （1）函数y=log₂（x-1）的图象是由y=log₂x的图象向右平移1个单位得到的；
（2）利用图象变换作出y=|log₂（x-1）|的图象．
（3）M=x₁x₂-2（x₁+x₂）+4=（x₁-2）（x₂-2）＜0，即可判断M的符号．

解答 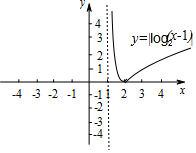解：（1）函数y=log₂（x-1）的图象是由y=log₂x的图象向右平移1个单位得到的．
（2）在右边的坐标系中作出y=|log₂（x-1）|的图象，如图所示；
（3）设函数y=${（\frac{1}{2}）}^{x}$与函数y=|log₂（x-1）|的图象的两个交点的横坐标分别为x₁，x₂，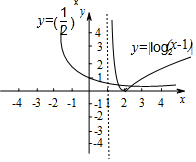

∴M=x₁x₂-2（x₁+x₂）+4=（x₁-2）（x₂-2）＜0．

点评 本题考查函数的图象，考查图象变换，考查学生分析解决问题的能力，正确作出函数的图象是关键．