
分析 (1)由椭圆的焦点在x轴上,c=2,根据椭圆的定义a=3,利用a与b和c之间的关系,即可求得椭圆的方程;
(2)由题意的焦点在y轴上,c=5,将点代入椭圆方程即可求得a和b的值,求得椭圆的方程.
解答 解:(1)由题意可知:椭圆的焦点在x轴上,设椭圆的标准方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),c=2,
椭圆上一点P到两焦点的距离之和等于6,即2a=6,则a=3,
b2=a2-c2=5,
∴椭圆的标准方程:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1$;
(2)由题意可知:椭圆的焦点在y轴上,设椭圆的标准方程:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0),c=5,
由a2=b2+c2=b2+25,
将P(3,4)代入椭圆方程:$\frac{{y}^{2}}{{b}^{2}+25}+\frac{{x}^{2}}{{b}^{2}}=1$,解得:b2=15,
∴椭圆的方程$\frac{{y}^{2}}{40}+\frac{{x}^{2}}{15}=1$.
点评 本题考查椭圆的标准方程及简单几何性质,考查待定系数法求椭圆的标准方程,考查计算能力,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=-sin 2x | B. | f(x)的图象关于x=-$\frac{π}{3}$对称 | ||
| C. | f($\frac{7π}{3}$)=$\frac{1}{2}$ | D. | f(x)的图象关于(1,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)函数y=log2(x-1)的图象是由y=log2x的图象如何变化得到的?
(1)函数y=log2(x-1)的图象是由y=log2x的图象如何变化得到的?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$与-λ$\overrightarrow{a}$的方向相反 | B. | |-λ$\overrightarrow{a}$|≥|$\overrightarrow{a}$| | ||
| C. | |-λ$\overrightarrow{a}$|=|λ|•$\overrightarrow{a}$ | D. | $\overrightarrow{a}$与λ2$\overrightarrow{a}$的方向相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
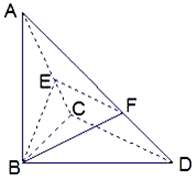 已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}$=λ(0<λ<1).
已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}$=λ(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com