
分析 设出P(x0,y0),得${x}_{0}•{y}_{0}=\frac{1}{4}$.再由圆系方程求出过两切点A,B的直线方程,分别求出M点,N点的坐标,代入三角形面积公式得答案.
解答 解:设P(x0,y0),则${x}_{0}•{y}_{0}=\frac{1}{4}$.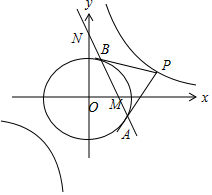
以OP为直径的圆的方程为$(x-\frac{{x}_{0}}{2})^{2}+(y-\frac{{y}_{0}}{2})^{2}=\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}}{4}$,
整理得:x2+y2-x0x-y0y=0,
又圆x2+y2=1,
两式作差可得x0x+y0y=1,即过A、B两切点的直线方程.
取y=0,得$x=\frac{1}{{x}_{0}}$,取x=0,得y=$\frac{1}{{y}_{0}}$.
∴${S}_{△OMN}=\frac{1}{2}|\frac{1}{{x}_{0}}||\frac{1}{{y}_{0}}|=\frac{1}{2}×\frac{1}{4}=\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 本题考查直线与圆位置关系的应用,考查数学转化思想方法和数形结合的解题思想方法,求出AB方程是关键,是中档题.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数$f(x)=sin\sqrt{x}$不是周期函数. | |
| B. | 函数$f(x)=sin\frac{1}{x}$不是周期函数. | |
| C. | 函数f(x)=sin|x|不是周期函数. | |
| D. | 函数f(x)=|sinx|+|cosx|的最小正周期为π. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com