
���� ��1������Բ��ͨ����ʽ��a=2c���������a��b��ֵ�����������Բ���̷��̣�
��2������ֱ�ߵ�б�ʹ�ʽ�����k1+k2=-$\frac{3{x}_{1}}{{2y}_{1}}$��k3+k4=$\frac{3{x}_{2}}{2{y}_{2}}$����$\overrightarrow{OP}$��$\overrightarrow{OQ}$���ߣ���$\frac{{x}_{1}}{{y}_{1}}$=$\frac{{x}_{2}}{{y}_{2}}$���������k1+k2+k3+k4=0��
��3��EF1��б��${k_1}^��$=$\frac{y}{\frac{{y}^{2}}{4}+1}$����y2��$\frac{8}{3}$��y��-2����EF2��б��${k_2}^��$=$\frac{y}{\frac{{y}^{2}}{4}-1}$����y2��$\frac{8}{3}$��y��2������$\frac{1}{{{k_1}^��{k_2}^��}}$=$\frac{{y}^{4}-16}{16{y}^{2}}$����y2��$\frac{8}{3}$��y�١�2�������ݺ��������Լ������$\frac{1}{{{k_1}^��{k_2}^��}}$��ȡֵ��Χ��
��� �⣺��1��������a=2c����Բ��ͨ��حABح=$\frac{{2b}^{2}}{a}$=3��
a2=b2+c2����a=2��b=$\sqrt{3}$��c=1��
����Բ�ı����̣�$\frac{x^2}{4}+\frac{y^2}{3}=1$��
��2���ɣ�1����֪��A��-2��0����B��2��0����F1��-1��0����F2��1��0������P��x1��y1����
��$\frac{{x}_{1}^{2}}{4}+\frac{{y}_{1}^{2}}{3}=1$����x12-4=-$\frac{4{y}_{1}^{2}}{3}$��k1+k2=$\frac{{y}_{1}}{{x}_{1}+2}$+$\frac{{y}_{1}}{{x}_{1}-2}$=$\frac{2{x}_{1}{y}_{1}}{{x}_{1}^{2}-4}$=$\frac{2{x}_{1}{y}_{1}}{-\frac{4{y}_{1}^{2}}{3}}$=-$\frac{3{x}_{1}}{{2y}_{1}}$����Q��x2��y2������$\frac{{x}_{2}^{2}}{4}-\frac{{y}_{2}^{2}}{3}=1$����x12-4=$\frac{4{y}_{1}^{2}}{3}$��
��k3+k4=$\frac{{y}_{2}}{{x}_{2}+2}$+$\frac{{y}_{2}}{{x}_{2}-2}$=$\frac{2{x}_{2}{y}_{2}}{{x}_{2}^{2}-4}$=$\frac{2{x}_{2}{y}_{2}}{\frac{4{y}_{2}^{2}}{3}}$=$\frac{3{x}_{2}}{2{y}_{2}}$��
��$\overrightarrow{OP}$��$\overrightarrow{OQ}$���ߣ�
��x1=��x2��y1=��y2��
��$\frac{{x}_{1}}{{y}_{1}}$=$\frac{{x}_{2}}{{y}_{2}}$��
k1+k2+k3+k4=$\frac{3}{2}$��-$\frac{{x}_{1}}{{y}_{1}}$+$\frac{{x}_{2}}{{y}_{2}}$��=0��
��3����E��$\frac{{y}^{2}}{4}$��y������$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{{y}^{2}=4x}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{x}^{2}=\frac{2}{3}}\\{{y}^{2}=\frac{8}{3}}\end{array}\right.$��
��E����ԲC���������K��y2=4x��һ�㣬��y2��$\frac{8}{3}$��
��EF1���${k_1}^��$=$\frac{y}{\frac{{y}^{2}}{4}+1}$����y2��$\frac{8}{3}$��y��-2����EF2���${k_2}^��$=$\frac{y}{\frac{{y}^{2}}{4}-1}$����y2��$\frac{8}{3}$��y��2��
��${k_1}^��$${k_2}^��$=$\frac{y}{\frac{{y}^{2}}{4}+1}$��$\frac{y}{\frac{{y}^{2}}{4}-1}$=$\frac{{y}^{2}}{��\frac{{y}^{2}}{4}��^{2}-1}$=$\frac{16{y}^{2}}{{y}^{4}-16}$����y2��$\frac{8}{3}$��y�١�2��
��$\frac{1}{{{k_1}^��{k_2}^��}}$=$\frac{{y}^{4}-16}{16{y}^{2}}$����y2��$\frac{8}{3}$��y�١�2��
��t=y2����t��$\frac{8}{3}$��t��4����
��f��t��=$\frac{{t}^{2}-16}{16t}$=$\frac{t}{16}$-$\frac{1}{t}$����t��$\frac{8}{3}$��t��4��������f�䣨t��=$\frac{1}{16}$+$\frac{1}{{t}^{2}}$��0
��f��t���ڣ�$\frac{8}{3}$��4������4��+�ޣ��ϵ���������
��f��t����ȡֵ��Χ��-$\frac{5}{24}$��0���ȣ�0��+�ޣ�
��$\frac{1}{{{k_1}^��{k_2}^��}}$��ȡֵ��Χ$��-\frac{5}{24}��0���ȣ�0��+�ޣ�$��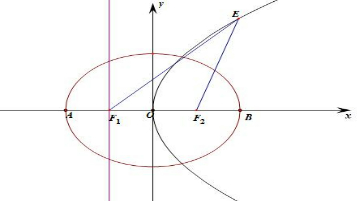
���� ���⿼����Բ�ı����̣�ֱ�ߵ�б�ʹ�ʽ����Բ��˫���ߵ����ʣ������������뵼���Ĺ�ϵ��������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?�ˣ�0��ʹ��$\overrightarrow c��\overrightarrow d$ | B�� | ?�ˣ�0��ʹ�ã�$\overrightarrow{c}$��$\overrightarrow{d}$��=60�� | ||
| C�� | ?�ˣ�0��ʹ�ã�$\overrightarrow{c}$��$\overrightarrow{d}$��=30�� | D�� | ?�ˣ�0��ʹ��$\overrightarrow c=m\overrightarrow d��m$Ϊ��Ϊ0�ij����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com