
分析 根据m>1,可以判断直线y=mx的倾斜角位于区间($\frac{π}{4}$,$\frac{π}{2}$)上,由此判断出满足约束条件的平面区域的形状,再根据目标函数z=x+my对应的直线与直线y=mx垂直,且在直线y=mx与直线x+y=1交点处取得最大值,由此可得关于m的函数表达式,根据函数的单调性,求出m的范围.
解答 解:∵m>1,由约束条件,作出可行域如图,
直线y=mx与直线x+y=1交于($\frac{1}{m+1}$,$\frac{m}{m+1}$),
目标函数z=x+my对应的直线与直线y=mx垂直,且在($\frac{1}{m+1}$,$\frac{m}{m+1}$)处取得最大值,
∴Z(m)=$\frac{1{+m}^{2}}{1+m}$,则z′(m)=$\frac{{(m+1)}^{2}-2}{{(m+1)}^{2}}$,
∵m>1,∴z′(m)>0,
∴函数z(m)在(1,+∞)上单调递增,
∴z(m)最小值>z(1)=1,
故答案为:($\frac{1}{m+1}$,$\frac{m}{m+1}$),(1,+∞).
点评 题考查的知识点是简单线性规划的应用,其中根据平面直线方程判断出目标函数z=x+my对应的直线与直线y=mx垂直,且在($\frac{1}{m+1}$,$\frac{m}{m+1}$)点取得最大值,并由此列出关于m的函数表达式是解答本题的关键,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
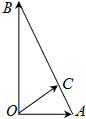
| A. | $\frac{1}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}$ | B. | $\frac{3}{4}\overrightarrow{OA}+\frac{1}{4}\overrightarrow{OB}$ | C. | $\frac{3}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ | D. | $\frac{5}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
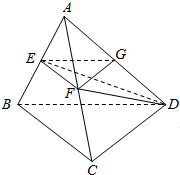 如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:
如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=4x3+x | B. | f(x)=ln$\frac{5-x}{5+x}$ | C. | f(x)=sin$\frac{x}{2}$ | D. | f(x)=ex+e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | $\frac{21}{3}$ | C. | $\frac{67}{6}$ | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com