
 如图,直三棱柱ABC-A1B1C1中,AA1=$\sqrt{2}$AB=$\sqrt{2}$BC=2,∠ABC=90°,D为CC1中点,则AB1与平面ABD所成角的正弦值是( )
如图,直三棱柱ABC-A1B1C1中,AA1=$\sqrt{2}$AB=$\sqrt{2}$BC=2,∠ABC=90°,D为CC1中点,则AB1与平面ABD所成角的正弦值是( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
分析 过B1作B1M⊥BD于M,连接AM,则可证B1M⊥平面ABD,故而∠B1AM为AB1与平面ABD所成的角,利用相似三角形及勾股定理计算AB1和B1M,即可得出sin∠B1AM.
解答 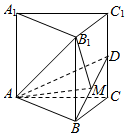 解:过B1作B1M⊥BD于M,连接AM.
解:过B1作B1M⊥BD于M,连接AM.
∵BB1⊥平面ABC,AB?平面ABC,
∴AB⊥BB1,又AB⊥BC,BB1∩BC=B,
∴AB⊥平面BCC1B1,∵B1M?平面BCC1B1,
∴AB⊥B1M.又B1M⊥BD,AB∩BD=B,
∴B1M⊥平面ABD.
∴∠B1AM为AB1与平面ABD所成的角.
∵AA1=$\sqrt{2}$AB=$\sqrt{2}$BC=2,
∴AB1=$\sqrt{6}$,CD=1,BC=$\sqrt{2}$,∴BD=$\sqrt{3}$.
∵△B1BM∽△BDC,∴$\frac{{B}_{1}M}{BC}=\frac{B{B}_{1}}{BD}$,∴B1M=$\frac{2\sqrt{6}}{3}$.
∴sin∠B1AM=$\frac{{B}_{1}M}{A{B}_{1}}$=$\frac{2}{3}$.
故选:A.
点评 本题考查了线面角的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | λ>1 | B. | λ<1 | C. | λ>-1 | D. | λ<-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 做不到“光盘”行动 | 做到“光盘”行动 | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
| A. | 有95%的把握认为“该学生能否做到光盘行到与性别有关” | |
| B. | 有95%的把握认为“该学生能否做到光盘行到与性别无关” | |
| C. | 有90%的把握认为“该学生能否做到光盘行到与性别有关” | |
| D. | 有90%的把握认为“该学生能否做到光盘行到与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{245}{128}$ | B. | $\frac{509}{256}$ | C. | $\frac{1003}{512}$ | D. | $\frac{2013}{1024}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com