
分析 设A(x1,y1),B(x2,y2),代入双曲线的方程,运用点差法,结合中点坐标公式和直线的斜率公式,由点斜式方程可得直线AB的方程,代入双曲线的方程,由判别式的符号,即可得到判断直线的存在性.
解答 解:设A(x1,y1),B(x2,y2),
可得x12-$\frac{{{y}_{1}}^{2}}{4}$=1,x22-$\frac{{{y}_{2}}^{2}}{4}$=1,
两式相减可得,(x1-x2)(x1+x2)-$\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{4}$=0,
M为AB的中点,即有x1+x2=4,y1+y2=2,
可得直线AB的斜率为k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{4({x}_{1}+{x}_{2})}{{y}_{1}+{y}_{2}}$=$\frac{4×4}{2}$=8,
即有直线AB的方程为y-1=8(x-2),即为8x-y-15=0.
由y=8x-15代入双曲线的方程x2-$\frac{{y}^{2}}{4}$=1,可得60x2-240x+229=0,
即有△=2402-4×60×229=240×11>0,故存在直线AB.
故答案为:y=8x-15.
点评 本题考查双曲线的中点弦所在直线方程的求法,注意运用点差法,注意检验直线的方程的存在性,考查运算能力,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
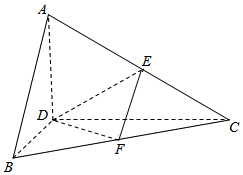 正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a,b∈R,且a+b>4,则a,b至少有一个大于2 | |
| B. | “?x0∈R,${2^{x_0}}=1$”的否定是“?x∈R,2x≠1” | |
| C. | a>1,b>1是ab>1的必要条件 | |
| D. | △ABC中,A是最大角,则sin2A>sin2B+sin2C是△ABC为钝角三角形的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-∞,-1)∪(3,+∞) | C. | (-1,3) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com