
分析 (Ⅰ)将A,B代入曲线C的方程,解方程组,可得m=4,n=1,即可得到所求曲线的方程;
(Ⅱ)设直线MN的方程为$y=kx+\frac{{\sqrt{3}}}{2}$,代入椭圆方程为y2+4x2=1,运用韦达定理,由向量的数量积的坐标表示,化简整理,解方程可得所求直线的斜率.
解答 解:(Ⅰ)将A,B代入曲线C的方程,可得:$\left\{\begin{array}{l}\frac{1}{8}m+\frac{1}{2}n=1\\ \frac{1}{6}m+\frac{1}{3}n=1\end{array}\right.$,
解得m=4,n=1.
所以曲线C方程为y2+4x2=1;
(Ⅱ)设直线MN的方程为$y=kx+\frac{{\sqrt{3}}}{2}$,代入椭圆方程为y2+4x2=1得,
$({k^2}+4){x^2}+\sqrt{3}kx-\frac{1}{4}=0$.
∴${x_1}+{x_2}=\frac{{-\sqrt{3}k}}{{{k^2}+4}},{x_1}{x_2}=\frac{{-\frac{1}{4}}}{{{k^2}+4}}$,
∴$\overrightarrow p•\overrightarrow q$=(2x1,y1)•(2x2,y2)=4x1x2+y1y2=0,
由y1y2=(kx1+$\frac{\sqrt{3}}{2}$)(kx2+$\frac{\sqrt{3}}{2}$)=k2x1x2+$\frac{3}{4}$+$\frac{\sqrt{3}}{2}$k(x1+x2),
∴$\frac{-1}{{{k^2}+4}}+\frac{{-\frac{1}{4}{k^2}}}{{{k^2}+4}}+\frac{{\frac{{\sqrt{3}}}{2}k•(-\sqrt{3}k)}}{{{k^2}+4}}+\frac{3}{4}=0$,
即${k^2}-2=0,k=±\sqrt{2}$.
点评 本题考查曲线的方程的求法,注意运用待定系数法,考查直线方程和椭圆方程联立,运用韦达定理和向量垂直的条件:数量积为0,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
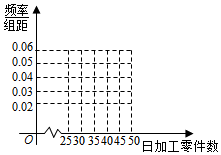 随机观测生产某种们零件的某工厂20名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,48,37,25,45,43,31,49,34,33,43,38,32,46,39,36.根据上述数据得到样本的频率分布表如下:
随机观测生产某种们零件的某工厂20名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,48,37,25,45,43,31,49,34,33,43,38,32,46,39,36.根据上述数据得到样本的频率分布表如下:| 分组 | 频数 | 频率 |
| [25,30] | 2 | 0.10 |
| (30,35] | 4 | 0.20 |
| (35,40] | 5 | 0.25 |
| (40,45] | m | fm |
| (45,50] | n | fn |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,$\frac{29}{4}$) | B. | (21,$\frac{135}{4}$) | C. | [27,30) | D. | (27,$\frac{135}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
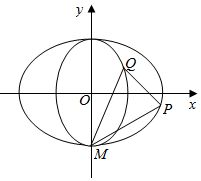 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点M(0,-$\sqrt{2}$),离心率为$\frac{\sqrt{2}}{2}$.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点M(0,-$\sqrt{2}$),离心率为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 37 | B. | 32 | C. | 35 | D. | 63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com