
分析 (Ⅰ)求出函数的对称轴小于-1,得到关于b,c的方程组,解出即可;
(Ⅱ)求出f(x)的对称轴,通过讨论对称轴的位置,结合函数的值域求出b,c的值,从而求出f(x)的表达式即可;
(Ⅲ)通过整理方程得到x2+(b-1)x+c=0或x2+(b+1)x+b+c+1=0,结合二次函数的性质进行证明即可.
解答 解:(Ⅰ)由条件知f(x)=x2+bx+c的最大值为5,最小值为-1
而b>2,则对称轴$x=-\frac{b}{2}<-1$,
则$\left\{\begin{array}{l}f({-1})=-1\\ f(1)=5\end{array}\right.$,即$\left\{\begin{array}{l}c-b+1=-1\\ b+c+1=5\end{array}\right.$,
解得$\left\{\begin{array}{l}c=1\\ b=3\end{array}\right.$
则f(x)=x2+3x+1.--------------------------------------------(3分)
(Ⅱ)f(x)=x2+bx+c,-1≤x≤0,对称轴x=-$\frac{b}{2}$,
若b≥2,则$x=-\frac{b}{2}≤-1$,则$\left\{\begin{array}{l}c-b+1=-1\\ c=0\end{array}\right.$,
解得$\left\{\begin{array}{l}c=0\\ b=2\end{array}\right.$,此时f(x)=x2+2x,
若b≤0,则$x=-\frac{b}{2}≥0$,则$\left\{\begin{array}{l}c-b+1=0\\ c=-1\end{array}\right.$,
解得$\left\{\begin{array}{l}c=-1\\ b=0\end{array}\right.$,此时f(x)=x2-1,
若0<b≤1,则$x=-\frac{b}{2}∈[{-\frac{1}{2},0})$,则$\left\{\begin{array}{l}c-b+1=0\\ c-\frac{b^2}{4}=-1\end{array}\right.$,
解得$\left\{\begin{array}{l}c=-1\\ b=0\end{array}\right.$(舍)或$\left\{\begin{array}{l}c=3\\ b=4\end{array}\right.$(舍),
此时不存在函数f(x),若1<b<2,则$x=-\frac{b}{2}∈({-1,-\frac{1}{2}})$,
则$\left\{\begin{array}{l}c=0\\ c-\frac{b^2}{4}=-1\end{array}\right.$,解得$\left\{\begin{array}{l}c=0\\ b=2\end{array}\right.$(舍)或$\left\{\begin{array}{l}c=0\\ b=-2\end{array}\right.$(舍),此时不存在函数f(x),
综上所述存在函数f(x)=x2-1和f(x)=x2+2x满足条件-----------------------------(8分)
(Ⅲ)由f(x)=x2+bx+c得f(f(x))=f2(x)+bf(x)+c及c=f(x)-x2-bx,
由f(f(x))=x得到f2(x)+bf(x)+c=x,即f2(x)+bf(x)+f(x)-x2-bx=x,
整理得到f2(x)-x2+b(f(x)-x)+(f(x)-x)=0,
即(f(x)-x)(f(x)+x+b+1)=0①
即f(x)-x=0或f(x)+x+b+1=0,
即x2+(b-1)x+c=0②或x2+(b+1)x+b+c+1=0③
方程②的判别式△=(b-1)2-4c
方程③的判别式${△_1}={({b+1})^2}-4b-4c-4={({b-1})^2}-4c-4=△-4$,
①若A≠ϕ,即f(x)-x=0有解,即x2+(b-1)x+c=0有解,即△≥0,则①有解,
即B≠ϕ,
②若A=ϕ,即△<0,则△1<0,②和③均无解,则①无解,即B=ϕ.----------------(12分)
点评 本题考查了二次函数的性质,考查函数的单调性、值域问题,考查求函数的解析式,以及集合问题,是一道综合题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 喜欢数学课 | 不喜欢数学课 | 合计 | |
| 男生 | 60 | 20 | 80 |
| 女生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
| A. | 4.762 | B. | 9.524 | C. | 0.0119 | D. | 0.0238 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”. | |
| B. | “若a,b∈R,则a-b>0⇒a>b”类比推出“若a,b∈C,则a-b>0⇒a>b”. | |
| C. | “若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈Q,则实数a+$\sqrt{3}$b=c+$\sqrt{3}$d⇒a=c,b=d” | |
| D. | “若a,b∈R,则|a+b|≤|a|+|b|”类比推出“若a,b∈C,则|a+b|≤|a|+|b|”. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
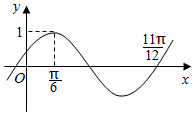 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则以下步骤可以得到函数f(x)的图象的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则以下步骤可以得到函数f(x)的图象的是( )| A. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向左平移$\frac{π}{6}$个单位 | |
| B. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向右平移$\frac{π}{6}$个单位 | |
| C. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的$\frac{1}{2}$,然后再向右平移$\frac{π}{12}$个单位 | |
| D. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的$\frac{1}{2}$,然后再向左平移$\frac{π}{12}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com