
【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重.该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数.f(t),随时刻t(时)变化的规律满足表达式![]() ,其中a为空气治理调节参数,且a∈(0,1).
,其中a为空气治理调节参数,且a∈(0,1).
(1)令![]() ,求x的取值范围;
,求x的取值范围;
(2)若规定每天中f(t)的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数a的取值范围.
【答案】(1)[0,1];(2)![]() .
.
【解析】
(1)题根据t的取值范围,及复合函数同增的单调性可得x的取值范围;
(2)题根据第(1)题的提示构造一个函数h(x)=|x-a|+3a+2,然后将绝对值函数转化成分段函数,考虑单调性及最大值的取值,再与5比较,即可得到调节参数a的取值范围.
(1)由题意,0≤t≤24,则1≤![]() t+1≤10,
t+1≤10,
∴0=lg1≤lg(![]() t+1)≤lg10=1.
t+1)≤lg10=1.
故x的取值范围为:[0,1].
(2)由(1),知: ![]()
可设![]()
则![]() .
.
根据一次函数的单调性,很明显h(x)在[0,a)上单调递减,在[a,1]上单调递增.
∴用![]() 表示函数的最大值是
表示函数的最大值是![]() 中最大的值.
中最大的值.
∵![]() ,
,
∴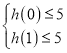 ,即
,即![]() ,
,
解得0<a≤![]() .
.
∴a的取值范围为:(0,![]() ].
].


科目:高中数学 来源: 题型:
【题目】以![]() 表示值域为
表示值域为![]() 的函数组成的集合,
的函数组成的集合,![]() 表示具有如下性质的函数
表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数
,存在一个正数![]() ,使得函数
,使得函数![]() 的值域包含于区间
的值域包含于区间![]() 。例如,当
。例如,当![]() ,
,![]() 时,
时,![]() ,
,![]() 。则下列命题中正确的是:( )
。则下列命题中正确的是:( )
A.设函数![]() 的定义域为
的定义域为![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ,
,![]() ,
,![]() ”
”
B.函数![]() 的充要条件是
的充要条件是![]() 有最大值和最小值
有最大值和最小值
C.若函数![]() ,
,![]() 的定义域相同,且
的定义域相同,且![]() ,
,![]() ,则
,则![]()
D.若函数![]() 有最大值,则
有最大值,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() 的参数方程是
的参数方程是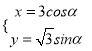 (
(![]() 为参数)以原点为极点,
为参数)以原点为极点, ![]() 轴正半轴为极轴,并取与直角坐标系相同的单位长度,建立极坐标系,曲线
轴正半轴为极轴,并取与直角坐标系相同的单位长度,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 和
和![]() 上的任意点,求
上的任意点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是改革开放四十周年大型展览的展馆--------国家博物馆.现欲测量博物馆正门柱楼顶部一点![]() 离地面的高度
离地面的高度![]() (点
(点![]() 在柱楼底部).在地面上的两点
在柱楼底部).在地面上的两点![]() ,
,![]() 测得点
测得点![]() 的仰角分别为
的仰角分别为![]() ,
,![]() ,且
,且![]() ,
,![]() 米,则
米,则![]() 为( )
为( )

A. 10米 B. 20米 C. 30米 D. 40米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提升城市道路通行能力,可为市民提供更多出行便利.我校某研究性学习小组对成都市一中心路段(限行速度为![]() 千米/小时)的拥堵情况进行调查统计,通过数据分析发现:该路段的车流速度
千米/小时)的拥堵情况进行调查统计,通过数据分析发现:该路段的车流速度![]() (辆/千米)与车流密度
(辆/千米)与车流密度![]() (千米/小时)之间存在如下关系:如果车流密度不超过
(千米/小时)之间存在如下关系:如果车流密度不超过![]() 该路段畅通无阻(车流速度为限行速度);当车流密度在
该路段畅通无阻(车流速度为限行速度);当车流密度在![]() 时,车流速度是车流密度的一次函数;车流密度一旦达到
时,车流速度是车流密度的一次函数;车流密度一旦达到![]() 该路段交通完全瘫痪(车流速度为零).
该路段交通完全瘫痪(车流速度为零).
(1)求![]() 关于
关于![]() 的函数
的函数![]()
(2)已知车流量(单位时间内通过的车辆数)等于车流密度与车流速度的乘积,求此路段车流量的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在[25,30),[55,60)的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(I)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(II)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某船在![]() 处测得灯塔
处测得灯塔![]() 在其南偏东
在其南偏东![]() 方向上,该船继续向正南方向行驶5海里到
方向上,该船继续向正南方向行驶5海里到![]() 处,测得灯塔在其北偏东
处,测得灯塔在其北偏东![]() 方向上,然后该船向东偏南
方向上,然后该船向东偏南![]() 方向行驶2海里到
方向行驶2海里到![]() 处,此时船到灯塔
处,此时船到灯塔![]() 的距离为多少海里( )
的距离为多少海里( )
A.![]() 千米B.
千米B.![]() 千米C.6千米D.5千米
千米C.6千米D.5千米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种蔬菜从1月1日起开始上市,通过市场调查,得到该蔬菜种植成本![]() (单位:元/
(单位:元/![]() )与上市时间
)与上市时间![]() (单位:10天)的数据如下表:
(单位:10天)的数据如下表:
时间 | 5 | 11 | 25 |
种植成本 | 15 | 10.8 | 15 |
(1)根据上表数据,从下列函数:![]() ,
,![]() ,
,![]() ,
,![]() 中(其中
中(其中![]() ),选取一个合适的函数模型描述该蔬菜种植成本
),选取一个合适的函数模型描述该蔬菜种植成本![]() 与上市时间
与上市时间![]() 的变化关系;
的变化关系;
(2)利用你选取的函数模型,求该蔬菜种植成本最低时的上市时间及最低种植成本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com