【题目】在三棱柱ABC﹣A1B1C1中，底面为正三角形，侧棱垂直底面，AB=2，AA1=6．若E，F分别是棱BB1 ， CC1上的点，且BE=B1E，C1F= 
CC1 ， 则异面直线A1E与AF所成角的余弦值为（ ） 
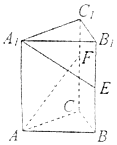
A.﹣ 
B.
C.﹣ 
D.
【答案】B
【解析】解：如图，取AB中点O，以O为原点，分别以OC，OA所在直线为x，y轴建立空间直角坐标系， ∵AB=2，AA1=6，BE=B1E，C1F= 
CC1 ，
∴A（0，1，0），F（ 
，0，4），A1（0，1，6），E（0，﹣1，3），
∴ 
， 
，
∴cos＜ 
＞= 
= 
．
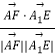∴异面直线A1E与AF所成角的余弦值为 
．
故选：B．
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识，掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．
科目：高中数学 来源： 题型：
【题目】已知a∈R，设命题p：指数函数y=ax（a＞0且a≠1）在R上单调递增；命题q：函数y=ln（ax2﹣ax+1）的定义域为R，若“p且q”为假，“p或q”为真，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知二次函数f（x）的对称轴x=﹣2，f（x）的图象被x轴截得的弦长为2 
，且满足f（0）=1．
（1）求f（x）的解析式；
（2）若f（（ 
）x）＞k，对x∈[﹣1，1]恒成立，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆O：x2+y2=4与x轴负半轴的交点为A，点P在直线l： 
x+y﹣a=0上，过点P作圆O的切线，切点为T．
（1）若a=8，切点T（ ，﹣1），求直线AP的方程；
（2）若PA=2PT，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P﹣ABCD中，底面是正方形，侧面PAD⊥底面ABCD，且PA=PD= 
AD，若E、F分别为PC、BD的中点．
（Ⅰ） 求证：EF∥平面PAD；
（Ⅱ） 求证：EF⊥平面PDC．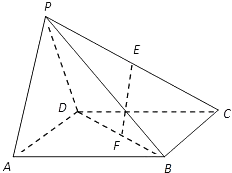
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P—ABCD中，PD
底面ABCD，AB//DC，ADDC，AB=AD=1，DC=2，PD=
，M为棱PB的中点．
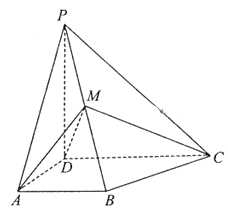
(1)证明：DM平面PBC；
(2)求二面角A—DM—C的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
