Question

20．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{3}}{2}$，且C过点Q（1，$\frac{\sqrt{3}}{2}$），
（Ⅰ）求曲线C的方程；
（Ⅱ）求曲线在点Q处的切线方程；
（Ⅲ）设点P（x₀，y₀）为圆x²+y²=5上任意一点，过点P向曲线C作切线，切点分别为A、B，试证明∠APB为定值．

Answer 1

分析 （Ⅰ）由题意知$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{3}{4{b}^{2}}=1}\\{e=\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{{b}^{2}+{c}^{2}={a}^{2}}\end{array}\right.$，从而解得；
（Ⅱ）当y≥0时，y=$\sqrt{1-\frac{{x}^{2}}{4}}$，从而求导确定切线的斜率，从而解得；
（Ⅲ）以切线是否垂直于坐标轴为标准分类讨论，当PA不垂直于坐标轴时，易知PB也不垂直于坐标轴，不妨设P（$\sqrt{5}$cosα，$\sqrt{5}$sinα），设切线方程为y-$\sqrt{5}$sinα=k（x-$\sqrt{5}$cosα），从而联立方程化简即可．

解答 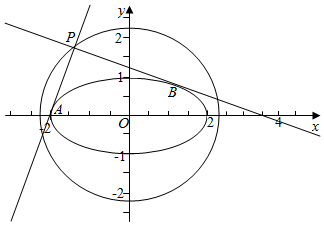解：（Ⅰ）由题意知，
$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{3}{4{b}^{2}}=1}\\{e=\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{{b}^{2}+{c}^{2}={a}^{2}}\end{array}\right.$，
解得，a=2，b=1；
故曲线C的方程为$\frac{{x}^{2}}{4}$+y²=1；
（Ⅱ）当y≥0时，y=$\sqrt{1-\frac{{x}^{2}}{4}}$，
y′=$\frac{-\frac{x}{2}}{2\sqrt{1-\frac{{x}^{2}}{4}}}$，
故y′|_x=1=$\frac{-\frac{1}{2}}{2\sqrt{1-\frac{1}{4}}}$=-$\frac{\sqrt{3}}{6}$，
故曲线在点Q处的切线方程为y-$\frac{\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{6}$（x-1），即x+2$\sqrt{3}$y-4=0；
（Ⅲ）证明：①当点P（-2，1），点P（-2，-1），点P（2，-1）或点P（2，1）时，
PA⊥PB，且两条切线分别垂直于坐标轴；
②当PA不垂直于坐标轴时，易知PB也不垂直于坐标轴，
不妨设P（$\sqrt{5}$cosα，$\sqrt{5}$sinα），设切线方程为y-$\sqrt{5}$sinα=k（x-$\sqrt{5}$cosα），
$\left\{\begin{array}{l}{y-\sqrt{5}sinα=k（x-\sqrt{5}cosα）}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$，
化简可得，
（4k²+1）x²+（8$\sqrt{5}$ksinα-8$\sqrt{5}$k²cosα）x+20k²cos²α+20sin²α-40ksinαcosα-4=0，
∵直线与椭圆相切，
∴△=（8$\sqrt{5}$ksinα-8$\sqrt{5}$k²cosα）²-4（4k²+1）（20k²cos²α+20sin²α-40ksinαcosα-4）=0，
化简可得，
（4-5cos²α）k²+10ksinαcosα+1-5sin²α=0，
设直线PA，PB的斜率为k₁，k₂，则
k₁k₂=$\frac{1-5si{n}^{2}α}{4-5co{s}^{2}α}$=$\frac{1-5（1-co{s}^{2}α）}{4-5co{s}^{2}α}$=-1，
故PA⊥PB，
综上所述，PA⊥PB，即∠APB为定值，∠APB=$\frac{π}{2}$．

点评 本题考查了圆锥曲线与直线的位置关系的判断与应用，同时考查了导数的综合应用及学生的化简运算能力．