
分析 先设β=α+$\frac{π}{6}$,根据sinβ求出cosβ,进而求出sin2β和cos2β,最后用两角和的正弦公式得到cos(2α+$\frac{π}{12}$)的值.
解答 解:设β=α+$\frac{π}{6}$,α为锐角,β=α+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{2π}{3}$),
∵sinβ=$\frac{3}{5}$<$\frac{\sqrt{3}}{2}$=sin$\frac{2π}{3}$,可得β为锐角,可求cosβ=$\frac{4}{5}$,sin2β=2sinβcosβ=$\frac{24}{25}$,cos2β=1-2sin2β=$\frac{7}{25}$,
∴cos(2α+$\frac{π}{12}$)=cos(2α+$\frac{π}{3}$-$\frac{π}{4}$)=cos(2β-$\frac{π}{4}$)=cos2βcos$\frac{π}{4}$+sin2βsin$\frac{π}{4}$=$\frac{31}{50}\sqrt{2}$.
故答案为:$\frac{31}{50}\sqrt{2}$.
点评 本题要我们在已知锐角α+$\frac{π}{6}$的余弦值的情况下,求2α+$\frac{π}{12}$的余弦函数值,着重考查了两角和与差的正弦、余弦公式和二倍角的正弦、余弦等公式,考查了三角函数中的恒等变换应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
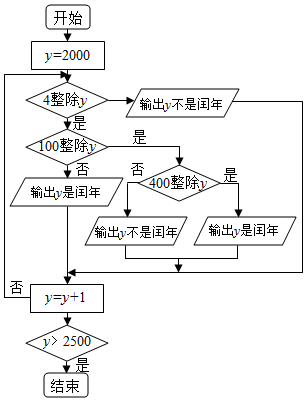
| A. | 输出年份y∈[2000,2500)且y∈N“哪年是闰年”“哪年不是闰年” | |
| B. | 输出年份y∈[2000,2500]且y∈N“哪年是闰年”“哪年不是闰年” | |
| C. | 输出年份y∈[2000,2500)且y∈N“多少年是闰年”“多少年不是闰年” | |
| D. | 输出年份y∈[2000,2500]且y∈N“多少年是闰年”“多少年不是闰年” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=-$\frac{4}{3}$,b=$\frac{1}{3}$ | B. | k=-$\frac{4}{3}$,b=-$\frac{1}{3}$ | C. | k=$\frac{4}{3}$,b=$\frac{1}{3}$ | D. | k=$\frac{4}{3}$,b=-$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com