
分析 (1)求导数,求出切线的斜率、切点的坐标,即可求f(x)在x=2处的切线方程;
(2)求导数,利用判别式,结合函数的单调性,即可求实数a的取值范围;
(2)确定当a=$\frac{1}{2}$时,令x=$\frac{n+1}{n}$,则$\frac{1}{2}$ln$\frac{n+1}{n}$>$\frac{1}{2n+1}$,累加可得结论.
解答 (1)解:当a=1时,f(x)=lnx-$\frac{x-1}{x+1}$,f′(x)=$\frac{1}{x}$-$\frac{2}{(x+1)^{2}}$…(1分)
∴f(2)=ln2-$\frac{1}{3}$,f′(2)=$\frac{5}{18}$…(3分)
∴f(x)在x=2处的切线方程为y=$\frac{5}{18}$x+ln2-$\frac{8}{9}$.…(4分)
(2)解:f′(x)=$\frac{a{x}^{2}+(2a-2)x+a}{x(x+1)^{2}}$,…(5分)
依题知f(1)=0,故f′(1)≥0,∴a≥$\frac{1}{2}$.…(6分)
令g(x)=ax2+(2a-2)x+a,△=-8a+4(a≥$\frac{1}{2}$),…(7分)
故g(x)≥0,a≥$\frac{1}{2}$,则f′(x)≥0,即f(x)在(1,+∞)上单调递增,…(8分)
又f(1)=0,∴a≥$\frac{1}{2}$.…(9分)
(3)证明:当a=$\frac{1}{2}$时,令x=$\frac{n+1}{n}$,则$\frac{1}{2}$ln$\frac{n+1}{n}$>$\frac{1}{2n+1}$,…(10分)
累加不等式,∴$\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2n+1}<\frac{1}{2}$ln(n+1)(n∈N*).…(12分)
点评 本题考查导数知识的综合运用,考查函数的单调性,考查不等式的证明,正确运用导数的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
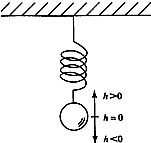 如图,弹簧挂着的小球上下振动,时间t(s)与小球相对于平衡位置(即静止时的位置)的高度h(cm)之间的函数关系式是h=$\sqrt{2}$sint+$\sqrt{2}$cost,t∈[0,+∞).,则小球开始振动时h的值为$\sqrt{2}$,小球振动时最大的高度差为4.
如图,弹簧挂着的小球上下振动,时间t(s)与小球相对于平衡位置(即静止时的位置)的高度h(cm)之间的函数关系式是h=$\sqrt{2}$sint+$\sqrt{2}$cost,t∈[0,+∞).,则小球开始振动时h的值为$\sqrt{2}$,小球振动时最大的高度差为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 14 | C. | 12 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.
如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com