练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．计算：$\frac{\sqrt{1+cos20°}}{2\sqrt{2}sin10°}$-sin10°（$\frac{1}{tan5°}$-tan5°）

    分析 由条件利用同角三角函数的基本关系，利用二倍角的正弦、余弦公式、和差化积公式进行化简要求的式子，从而得到结果．

    解答 解：：$\frac{\sqrt{1+cos20°}}{2\sqrt{2}sin10°}$-sin10°（$\frac{1}{tan5°}$-tan5°）=$\frac{\sqrt{2}•cos10°}{2\sqrt{2}sin10°}$-sin10°（$\frac{cos5°}{sin5°}$-$\frac{sin5°}{cos5°}$）
    =$\frac{cos10°}{2sin10°}$-sin10°•$\frac{{cos}^{2}5°{-sin}^{2}5°}{sin5°cos5°}$
    =$\frac{cos10°}{2sin10°}$-sin10°•$\frac{cos10°}{\frac{1}{2}sin10°}$=$\frac{cos10°}{2sin10°}$-2cos10°=$\frac{1}{2}$cot10°-2cos10°
    =$\frac{cos10°-4sin10°cos10°}{2sin10°}$=$\frac{sin80°-sin20°-sin20°}{2sin10°}$=$\frac{2cos50°sin30°-sin20°}{2sin10°}$=$\frac{sin40°-sin20°}{2sin10°}$
    =$\frac{2cos30°sin10°}{2sin10°}$=cos30°=$\frac{\sqrt{3}}{2}$．

    点评 本题主要考查利用同角三角函数的基本关系，和差化积公式的应用，利用二倍角的正弦、余弦公式进行化简求值，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=alnx-$\frac{x-1}{x+1}$．
    （1）当a=1时，求f（x）在x=2处的切线方程；
    （2）当x＞1时，f（x）＞0，求实数a的取值范围；
    （3）证明：$\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2n+1}＜\frac{1}{2}$ln（n+1）（n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．各项均为实数的等差数列的公差为2，其首项的平方与其余各项之和不超过33，则这样的数列至多有7项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在平面直角坐标系xoy中，设点P（x0，y0）为椭圆Γ：$\frac{x^2}{4}+\frac{y^2}{3}=1$上一点，过点P的直线${l_1}：\frac{{{x_0}x}}{4}+\frac{{{y_0}y}}{3}=1$交直线l2：x=4于点Q．
    （1）证明：直线l1为椭圆Γ的切线；
    （2）x轴上是否存在定点R，使得以PQ为直径的圆过定点R？若存在，求出R的坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

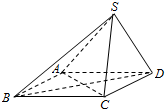    13．已知在四棱锥S-ABCD中，底面ABCD是平行四边形，若SB⊥AC，SA=SC．
    （1）求证：平面SBD⊥平面ABCD；
    （2）若AB=2，SB=3，cos∠SCB=-$\frac{1}{8}$，∠SAC=60°，求四棱锥S-ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知直线l：y=x+2与双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）相交于B、D两点，且BD的中点为M（1，3）．
    （1）求双曲线C的离心率；
    （2）设双曲线C的右顶点为A，右焦点为F，|BF|•|DF|=17，试判断△ABD是否为直角三角形，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

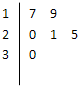    10．某车间共有12名工人，随机抽取6名作为样本，他们某日加工零件的个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．
    （1）根据茎叶图计算样本均值；
    （2）根据茎叶图推断该车间12名工人中有几名优秀工人；
    （3）要从这6人中，随机选出2人参加一项技术比武，选出的2人至少有1人为优秀工人的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．某地区有小学18所，中学12所，大学6所，现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查．
    （1）若从抽取的6所学校中随机抽取2所学校做进一步数据分析，求抽取的2所学校均为小学的概率；
    （2）若某小学被抽取，该小学五个年级近视眼率y的数据如下表：
    年级号x12345
    近视眼率y0.10.150.20.30.39
    根据前四个年级的数据，利用最小二乘法求y关于x的线性回归直线方程，并计算五年级近视眼率的估计值与实际值之间的差的绝对值．
    （附：回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘法估计公式分别为：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，右焦点到直线y=x+$\sqrt{6}$的距离为2$\sqrt{3}$．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）已知点M（2，1），斜率为$\frac{1}{2}$的直线l交椭圆E于两个不同点A，B，设直线MA与MB的斜率分别为k1，k2．
    ①若直线l过椭圆的左顶点，求k1，k2的值；
    ②试猜测k1，k2的关系，并给出你的证明．

    查看答案和解析>>

    同步练习册答案