
分析 (1)利用导数的几何意义得到直线的斜率,然后由点斜式得到直线方程;
(2)利用定积分表示曲边梯形的面积,然后计算即可.
解答 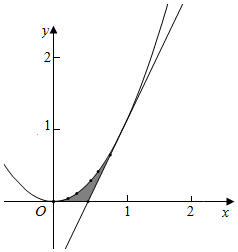 解:(1)因为y=x2在x=1处的切线为l,
解:(1)因为y=x2在x=1处的切线为l,
所以直线斜率为2,又切点为(1,1),所以直线方程为:2x-y-1=0;
(2)直线l与曲线C交点为(1,1),它们以及x轴所围成的图形如图
面积为S=${∫}_{0}^{1}({x}^{2}-2x+1)dx$-$\frac{1}{2}×\frac{1}{2}×1$=($\frac{1}{3}{x}^{3}-{x}^{2}+x$)|${\;}_{0}^{1}$$-\frac{1}{2}×\frac{1}{2}×1$=$\frac{1}{12}$,
所以$S=\frac{1}{12}$.
点评 本题考查了导数的几何意义以及利用定积分求曲边梯形的面积;关键是利用定积分表示出曲边梯形的面积,然后正确计算.


科目:高中数学 来源: 题型:选择题

| A. | 四棱锥四个侧面中不存在两组侧面互相垂直 | |
| B. | 四棱锥的四个侧面可能全是直角三角形 | |
| C. | 若该四棱锥的左视图为直角三角形,则体积为$\frac{4}{3}$ | |
| D. | 若该四棱锥的正视图为等腰三角形,则四棱锥的侧面积为6+2$\sqrt{2}$+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
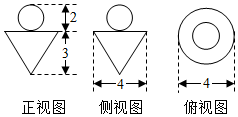
| A. | 5π | B. | $\frac{40π}{3}$ | C. | $\frac{20π}{3}$ | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
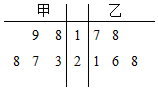 甲、乙两名运动员的5次测试成绩如图,设s1,s2分别表示甲、乙两名运动员测试成绩的标准差,$\overline{{x}_{1}}$,$\overline{{x}_{2}}$分别表示甲、乙两名运动员测试成绩的平均数,则有( )
甲、乙两名运动员的5次测试成绩如图,设s1,s2分别表示甲、乙两名运动员测试成绩的标准差,$\overline{{x}_{1}}$,$\overline{{x}_{2}}$分别表示甲、乙两名运动员测试成绩的平均数,则有( )| A. | $\overline{{x}_{1}}>\overline{{x}_{2}}$,s1>s2 | B. | $\overline{{x}_{1}}<\overline{{x}_{2}}$,s1>s2 | C. | $\overline{{x}_{1}}<\overline{{x}_{2}}$,s1<s2 | D. | $\overline{{x}_{1}}>\overline{{x}_{2}}$,s1<s2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com