
分析 (1)利用三角恒等变换化简函数f(x)为正弦型函数,按五个关键点列表,描点并用光滑的曲线连接成图,由图写出f(x)的单调递减区间;
(2)由(1)中所作的函数图象,求出f(x)在$x∈[{0,\frac{π}{2}}]$时的最值.
解答 解:(1)因为函数$f(x)=sin({2x+\frac{π}{6}})+2{cos^2}x$
=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x+cos2x+1
=$\sqrt{3}({\frac{1}{2}sin2x+\frac{{\sqrt{3}}}{2}cos2x})+1$
=$\sqrt{3}({sin2xcos\frac{π}{3}+cos2xsin\frac{π}{3}})+1$
=$\sqrt{3}sin({2x+\frac{π}{3}})+1$,
所以$f(x)=\sqrt{3}sin({2x+\frac{π}{3}})+1$,
按五个关键点列表,得
| $2x+\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $-\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| y | 1 | $1+\sqrt{3}$ | 1 | $1-\sqrt{3}$ | 1 |
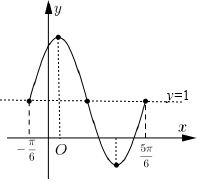
点评 本题考查了三角恒等变换与五点法画图问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题¬p是真命题 | |
| B. | 命题p是特称命题 | |
| C. | 命题p是全称命题 | |
| D. | 命题p既不是全称命题也不是特称命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )
已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )| A. | x2=4y | B. | x2=2$\sqrt{3}$y | C. | x2=6y | D. | x2=2$\sqrt{2}$y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com