
���� ��1�����ԲF1��Բ�ĺͰ뾶������ƽ���ߵ����ʺ͵��������ε����ʣ��ɵ�ED=EF2������˫���ߵĶ��壬���ɵõ�����ֵ��˫���ߵķ��̣�
��2�����l��x=my+2��m��0����lPQ��y=-m��x-2������M��x1��y1����N��x2��y2�������Բ�ĵ�ֱ��PQ�ľ��룬�����ҳ���ʽ�ɵ�|PQ|������ֱ��l�ķ��̺�˫���ߵķ�������������Τ�ﶨ�����ҳ���ʽ���ɵ�|MN|�����������ε������ʽ�ɵá�PQM���PQN�����֮��Ϊ$\frac{1}{2}$|MN|•|PQ|��������������ϲ���ʽ�����ʣ����ɵõ�����Χ��
��� �⣺��1��֤����Բ${F_1}��{��{x+2}��^2}+{y^2}=4$��Բ��F1��-2��0�����뾶r=2����ͼ��ʾ��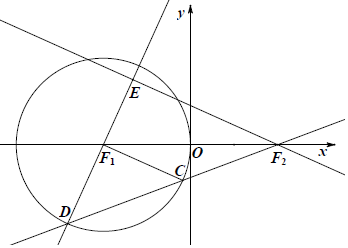
��ΪF1C��EF2�����ԡ�F1CD=��EF2D��
����ΪF1D=F1C�����ԡ�F1CD=��F1DC��
���ԡ�EF2D=��F1DC��
����Ϊ��F1DC=��EDF2�����ԡ�EF2D=��EDF2��
��ED=EF2���ɵ�||EF1|-|EF2||=||EF1|-|ED||=|F1D|=2��|F1F2|��
����˫���ߵĶ��壬��֪��E�Ĺ켣����F1��F2Ϊ�����˫���ߣ�������⣩��
��a=1��c=2��b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$��
�ʵ�E�Ĺ켣����Ϊ${x^2}-\frac{y^2}{3}=1��{y��0}��$��
��2��$����{x^2}-\frac{y^2}{3}=1��{y��0}��$��
���������l��x=my+2��m��0����M��x1��y1����N��x2��y2����
����PQ��l����lPQ��y=-m��x-2����
Բ��F1��-2��0����ֱ��PQ�ľ���$d=\frac{{|{-m��{-2-2}��}|}}{{\sqrt{1+{m^2}}}}=\frac{{|{4m}|}}{{\sqrt{1+{m^2}}}}$��
����$|{PQ}|=2\sqrt{{r^2}-{d^2}}=\frac{{4\sqrt{1-3{m^2}}}}{{\sqrt{1+{m^2}}}}$��
����Ϊd��2�����$0��{m^2}��\frac{1}{3}$��
����ֱ��l��˫���ߦ��ķ���$\left\{{\begin{array}{l}{{x^2}-\frac{y^2}{3}=1}\\{x=my+2}\end{array}}\right.$����ȥx�ã�3m2-1��y2+12my+9=0��
��${y_1}+{y_2}=-\frac{12m}{{3{m^2}-1}}��{y_1}{y_2}=\frac{9}{{3{m^2}-1}}$��
����$|{MN}|=\sqrt{1+{m^2}}|{{y_2}-{y_1}}|=\sqrt{1+{m^2}}\sqrt{{{��{{y_1}+{y_2}}��}^2}-4{y_1}{y_2}}=\frac{{6��{{m^2}+1}��}}{{1-3{m^2}}}$��
�ǡ�PQM����PQN������ֱ�ΪS1��S2��
��${S_1}+{S_2}=\frac{1}{2}|{MN}|•|{PQ}|=\frac{{12\sqrt{{m^2}+1}}}{{\sqrt{1-3{m^2}}}}=12\sqrt{\frac{1}{{-3+\frac{4}{{{m^2}+1}}}}}$��
����Ϊ$0��{m^2}��\frac{1}{3}$������S1+S2�ʣ�12��+�ޣ���
����S1+S2��ȡֵ��ΧΪ��12��+�ޣ���
���� ���⿼��켣���̵���ע������˫���ߵĶ��壬����ֱ�ߺ�Բ��ֱ�ߺ���Բ��λ�ù�ϵ��ע�����������飬����Τ�ﶨ�����ҳ���ʽ��������������������Լ��������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow{a}$��$\overrightarrow{b}$ | B�� | $\overrightarrow{a}$��$\overrightarrow{b}$ | C�� | |$\overrightarrow{a}$|=2|$\overrightarrow{b}$|| | D�� | ��$\overrightarrow{a}$��$\overrightarrow{b}$��=60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{1}{256}$ | C�� | 64 | D�� | $\frac{1}{64}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $\sqrt{7}$ | C�� | 3 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{8}{5}$ | B�� | $\frac{9}{5}$ | C�� | $-\frac{9}{5}$ | D�� | $\frac{8}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 21 | B�� | -21 | C�� | 441 | D�� | -441 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com