
| A. | $[{-\frac{lnπ}{π},0}]$ | B. | [-πlnπ,0] | C. | $[{-\frac{1}{e},\frac{lnπ}{π}}]$ | D. | $[{-\frac{e}{2},-\frac{1}{π}}]$ |
分析 由题意,找出x∈(1,π]的解析式,画出f(x)定义在$[{\frac{1}{π},π}]$上的图形,利用直线y=ax与f(x)的交点个数得到a的范围.
解答  解:因为当$x∈[{\frac{1}{π},1}]$时,f(x)=lnx,
解:因为当$x∈[{\frac{1}{π},1}]$时,f(x)=lnx,
所以x∈(1,π]时,$\frac{1}{x}∈[\frac{1}{π},1]$,所以f($\frac{1}{x}$)=-lnx,此时$f(x)=f(\frac{1}{x})$,故f(x)=-lnx,x∈(1,π].
所以f(x)在$[{\frac{1}{π},π}]$上的图象如图,要使函数g(x)=f(x)-ax在$[{\frac{1}{π},π}]$上有零点,只要直线y=ax与f(x)的图象有交点,
由图象可得,kOA≤a≤0,其中${k}_{OA}=\frac{ln\frac{1}{π}}{\frac{1}{π}}=-πlnπ$,
所以使函数g(x)=f(x)-ax在$[{\frac{1}{π},π}]$上有零点,则实数a的取值范围是[-πlnπ,0].
故选:B.
点评 本题考查通过将定义域转变到已知函数的定义域上求函数解析式的方法,数形结合解题的方法,关键是将零点个数转化为函数图象的交点个数解答.


科目:高中数学 来源: 题型:解答题
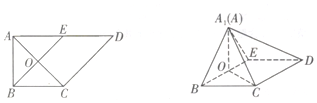 如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙
如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)>f(b)>f(c) | B. | f(a)>f(c)>f(b) | C. | f(b)>f(a)>f(c) | D. | f(c)>f(a)>f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
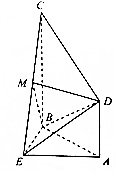 如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=$\frac{1}{2}$BC=2,M是EC的中点.
如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=$\frac{1}{2}$BC=2,M是EC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com