
分析 直线l:y=ax+2上任意一点(x,y),(x′,y′)是所得的直线上一点,根据矩阵变换特点,写出两对坐标之间的关系,把已知的点的坐标代入得到直线的方程,得到结果.
解答 解:设P(x,y)为直线l上任意一点,在矩阵A对应的变换下变为直线l′上点P′(x′,y′),则$[\begin{array}{l}{x′}\\{y′}\end{array}]$=$[\begin{array}{l}{0}&{1}\\{1}&{-2}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$,
化简,得$\left\{\begin{array}{l}{x=2x′+y′}\\{y=x′}\end{array}\right.$
代入l:y=ax+2,整理,得x′=a(2x′+y′)+2.
将点(1,1)代入上述方程,解得a=-$\frac{1}{3}$.
故答案为-$\frac{1}{3}$.
点评 本题主要考查二阶矩阵的变换,考查运算求解能力,比较基础.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,4] | B. | [4,+∞) | C. | (0,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
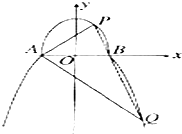 如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.
如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在梯形ABCD中,AD∥BC,∠ABC=90°,AB=a,AD=3a,且∠ADC=arcsin$\frac{{\sqrt{5}}}{5}$,PA⊥平面ABCD,PA=a,则二面角P-CD-A的大小为arctan$\frac{\sqrt{5}}{3}$.
在梯形ABCD中,AD∥BC,∠ABC=90°,AB=a,AD=3a,且∠ADC=arcsin$\frac{{\sqrt{5}}}{5}$,PA⊥平面ABCD,PA=a,则二面角P-CD-A的大小为arctan$\frac{\sqrt{5}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
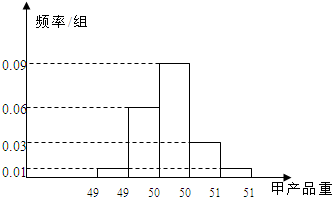 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:| 乙流水线 产品重量(单位:克) | 频数 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com