
分析 如图所示,在△PF1F2中,由正弦定理可得:$\frac{|P{F}_{1}|}{sin∠P{F}_{2}{F}_{1}}$=$\frac{|P{F}_{2}|}{sin∠P{F}_{1}{F}_{2}}$,利用已知$\frac{a}{sin∠P{F}_{1}{F}_{2}}$=$\frac{c}{sin∠P{F}_{2}{F}_{1}}$,可得$\frac{c}{a}$=$\frac{|P{F}_{1}|}{|P{F}_{2}|}$<1,由椭圆的定义可得:|PF1|+|PF2|=2a,a<|PF2|≤a+c,化简整理即可得出.
解答 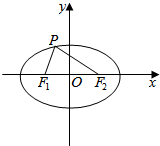 解:如图所示,
解:如图所示,
在△PF1F2中,由正弦定理可得:$\frac{|P{F}_{1}|}{sin∠P{F}_{2}{F}_{1}}$=$\frac{|P{F}_{2}|}{sin∠P{F}_{1}{F}_{2}}$,
又已知$\frac{a}{sin∠P{F}_{1}{F}_{2}}$=$\frac{c}{sin∠P{F}_{2}{F}_{1}}$,
∴$\frac{c}{a}$=$\frac{|P{F}_{1}|}{|P{F}_{2}|}$<1,
∵|PF1|+|PF2|=2a,a<|PF2|≤a+c,
∴∴$\frac{c}{a}$=$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\frac{2a-|P{F}_{2}|}{|P{F}_{2}|}$=$\frac{2a}{|P{F}_{2}|}$-1,
∴$\frac{1}{a+c}$≤$\frac{1}{|P{F}_{2}|}$<$\frac{1}{a}$,
∴$\frac{a-c}{a+c}$≤$\frac{c}{a}$<1,即$\frac{1-e}{1+e}$≤e<1,
解得$\sqrt{2}-1$<e<1.
∴椭圆的离心率的取值范围为$[\sqrt{2}-1,1)$.
故答案为:$[\sqrt{2}-1,1)$.
点评 本题考查了椭圆的性质、不等式的性质、正弦定理,考查了推理能力与计算能力,属于中档题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
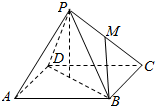 已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.
已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com