
分析 由条件利用同角三角函数的基本关系求得tanθ的值,再利用两角和的正切公式求得tan(θ十$\frac{π}{4}$)的值.
解答 解:∵sinθ-2cosθ=$\sqrt{5}$,∴平方可得 1+3cos2θ-4sinθcosθ=5,即 $\frac{{3cos}^{2}θ-4sinθcosθ}{{sin}^{2}θ{+cos}^{2}θ}$=4,
即 $\frac{3-4tanθ}{{tan}^{2}θ+1}$=4,求得tanθ=-$\frac{1}{2}$ 则tan(θ十$\frac{π}{4}$)=$\frac{tanθ+1}{1-tanθ}$=$\frac{\frac{1}{2}}{\frac{3}{2}}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题主要考查同角三角函数的基本关系,两角和的正切公式,属于基础题.


科目:高中数学 来源: 题型:选择题
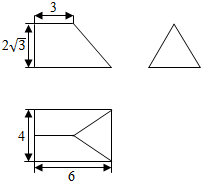
| A. | 60+4$\sqrt{3}$+2$\sqrt{21}$ | B. | 60+2$\sqrt{3}$+2$\sqrt{21}$ | C. | 60+2$\sqrt{3}$+4$\sqrt{21}$ | D. | 60+4$\sqrt{3}$+4$\sqrt{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)>f $({{{log}_{0.5}}\frac{1}{4}})$>f(lg0.5) | B. | f(lg0.5)>f(-1)>f $({{{log}_{0.5}}\frac{1}{4}})$ | ||
| C. | f $({{{log}_{0.5}}\frac{1}{4}})$>f(-1)>f(lg0.5) | D. | f(lg0.5)>f $({{{log}_{0.5}}\frac{1}{4}})$>f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器,圆锥的上底圆周与鱼缸的底面正方形相切,圆锥的顶点在鱼缸的缸底上,现在向鱼缸内随机地投入一粒鱼食,则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是( )
如图,在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器,圆锥的上底圆周与鱼缸的底面正方形相切,圆锥的顶点在鱼缸的缸底上,现在向鱼缸内随机地投入一粒鱼食,则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是( )| A. | 1-$\frac{π}{4}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com