
分析 设z=x+yi(x,y∈R),求得$\overline{z}$与|z|,代入$\overline z+|z|i=3+2i$,利用复数相等的条件得到关于x,y的方程组,求解方程组得答案.
解答 解:设z=x+yi(x,y∈R),
则$\overline{z}=x-yi$,$|z|=\sqrt{{x}^{2}+{y}^{2}}$,
代入$\overline z+|z|i=3+2i$,
得$x-yi+\sqrt{{x}^{2}+{y}^{2}}i=3+2i$,
即$\left\{\begin{array}{l}{x=3}\\{\sqrt{{x}^{2}+{y}^{2}}-y=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=\frac{5}{4}}\end{array}\right.$,
∴$z=3+\frac{5}{4}i$.
点评 本题考查复数代数形式的混合运算,考查了复数相等的条件,是基础的计算题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
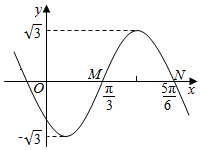 如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.
如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com