
| A. | 若α⊥β,m∥α,则m⊥β | B. | 若m?α,n?β,且m⊥n,则α⊥β | ||
| C. | 若α∥β,β∥λ,则α∥λ | D. | 若m∥α,n∥α,则m∥n |
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
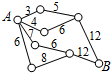 如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 19 | B. | 20 | C. | 24 | D. | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{{\begin{array}{l}{{x^2}-1,x<1}\\{-{{log}_2}x,x≥1}\end{array}}$.
已知函数f(x)=$\left\{{\begin{array}{l}{{x^2}-1,x<1}\\{-{{log}_2}x,x≥1}\end{array}}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com