
分析 (I)在△ABC中,由cosB=$\frac{2\sqrt{5}}{5}$,B为锐角,可得tanB,又tanC=$\frac{1}{3}$,利用tan(B+C)=$\frac{tanB+tanC}{1-tanBtanC}$即可得出.
(II) 0°<A<180°,由(I)结论可得:A=135°.在△ABC中,B,C均为锐角,可得cosB,tanC,sinB,sinC,再利用正弦定理可得a,即可得出△BAC的面积S=$\frac{1}{2}$acsin B.
解答 解:(I)在△ABC中,∵cosB=$\frac{2\sqrt{5}}{5}$,B为锐角,tanB=$\frac{1}{2}$,
又tanC=$\frac{1}{3}$,tan(B+C)=$\frac{tanB+tanC}{1-tanBtanC}$=$\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2}×\frac{1}{3}}$=1,
∴tanA=tan(180°-(B+C))=-tan(B+C),
故tanA=-1.
(II)∵0°<A<180°,由(I)结论可得:A=135°.
∴在△ABC中,B,C均为锐角,∵$cosB=\frac{{2\sqrt{5}}}{5}$,$tanC=\frac{1}{3}$,
∴$sinB=\frac{{\sqrt{5}}}{5}$,$sinC=\frac{{\sqrt{10}}}{10}$.
由$\frac{a}{sinA}=\frac{c}{sinC}$,得$a=\sqrt{5}$.
故△BAC的面积为:S=$\frac{1}{2}$acsin B=$\frac{1}{2}$.
点评 本题考查了三角函数就不关系式、和差公式、正弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
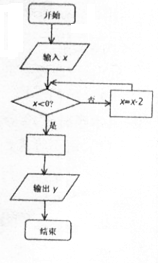 如图是一个算法程序框图,当输入的x的值为4时,输出的结果恰好是$\frac{1}{4}$,则空白处的关系式可以是( )
如图是一个算法程序框图,当输入的x的值为4时,输出的结果恰好是$\frac{1}{4}$,则空白处的关系式可以是( )| A. | y=2-x | B. | y=2x | C. | y=x${\;}^{-\frac{1}{2}}$ | D. | y=x${\;}^{\frac{1}{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若{an}是等差数列,且首项a1=0,则{an}是“和有界数列” | |
| B. | 若{an}是等差数列,且公差d=0,则{an}是“和有界数列” | |
| C. | 若{an}是等比数列,且公比|q|<1,则{an}是“和有界数列” | |
| D. | 若{an}是等比数列,且{an}是“和有界数列”,则{an}的公比|q|<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,m∥α,则m⊥β | B. | 若m?α,n?β,且m⊥n,则α⊥β | ||
| C. | 若α∥β,β∥λ,则α∥λ | D. | 若m∥α,n∥α,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 216-1 | B. | 216-2 | C. | 216-3 | D. | 216-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com