
分析 (Ⅰ)由题意,可求得a2,再由a2的值求a3,再由a3 的值求出a4的值.
(Ⅱ)猜想检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答 解:(Ⅰ)当n=2时,a1+a2=6a2,解得a2=$\frac{1}{15}$;
当n=3时,a1+a2+a3=15a3,解得a3=$\frac{1}{35}$;
当n=4时,a1+a2+a3+a4=28a4,解得a4=$\frac{1}{63}$.
(Ⅱ)∴a1=$\frac{1}{3}$=$\frac{1}{1×3}$,a2=$\frac{1}{15}$=$\frac{1}{3×5}$,a3=$\frac{1}{35}$=$\frac{1}{5×7}$,a4=$\frac{1}{63}$=$\frac{1}{7×9}$,
故猜想an=$\frac{1}{(2n-1)(2n+1)}$.
下面用数学归纳法证明:
①当n=1时,由已知显然成立
②设当n=k时,结论成立,即ak=$\frac{1}{(2k-1)(2k+1)}$
当n=k+1时,∵Sk+1=Sk+ak+1=(k+1)(2k+1)ak+1,…(﹡)
又Sk=k(2k-1)ak=k(2k-1)•$\frac{1}{(2k-1)(2k+1)}$=$\frac{k}{2k+1}$代入(﹡)式得$\frac{k}{2k+1}$+ak+1=(k+1)(2k+1)ak+1,
解得ak+1=$\frac{1}{(2k+1)(2k+3)}$,由以上归纳证明可知猜想成立.
点评 本题考查数列的递推公式,用数学归纳法证明等式成立.证明当n=k+1时命题也成立,是解题的难点.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
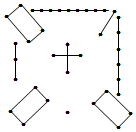 洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.
洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com