
(本题12分)已知函数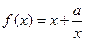 有如下性质:如果常数
有如下性质:如果常数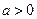 ,那么该函数在
,那么该函数在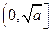 上是减函数,在
上是减函数,在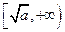 上是增函数;
上是增函数;
(1)如果函数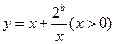 在
在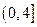 上是减函数,在
上是减函数,在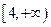 上是增函数,求
上是增函数,求 的值;
的值;
(2)当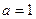 时,试用函数单调性的定义证明函数f(x)在
时,试用函数单调性的定义证明函数f(x)在 上是减函数。
上是减函数。
(3)设常数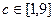 ,求函数
,求函数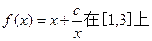 的最大值和最小值;
的最大值和最小值;
科目:高中数学 来源: 题型:解答题
(本小题满分 分)
分)
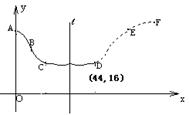
在股票市场上,投资者常参考 股价(每一股的价格)的某条平滑均线(记作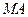 )的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的
)的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的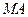 均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系
均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系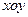 ,则股价
,则股价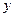 (元)和时间
(元)和时间 的关系在
的关系在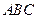 段可近似地用解析式
段可近似地用解析式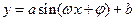 (
(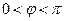 )来描述,从
)来描述,从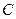 点走到今天的
点走到今天的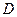 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且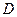 点和
点和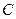 点正好关于直线
点正好关于直线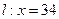 对称.老张预计这只股票未来的走势如图中虚线所示,这里
对称.老张预计这只股票未来的走势如图中虚线所示,这里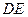 段与
段与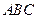 段关于直线
段关于直线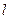 对称,
对称, 段是股价延续
段是股价延续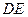 段的趋势(规律)走到这波上升行情的最高点
段的趋势(规律)走到这波上升行情的最高点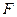 .
.
现在老张决定取点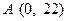 ,点
,点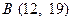 ,点
,点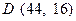 来确定解析式中的常数
来确定解析式中的常数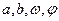 ,并且已经求得
,并且已经求得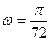 .
.
(Ⅰ)请你帮老张算出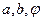 ,并回答股价什么时候见顶(即求
,并回答股价什么时候见顶(即求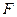 点的横坐标).
点的横坐标).
(Ⅱ)老张如能在今天以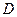 点处的价格买入该股票
点处的价格买入该股票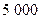 股,到见顶处
股,到见顶处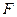 点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)已知集合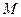 是满足下列性质的函数
是满足下列性质的函数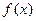 的全体:在定义域内存在
的全体:在定义域内存在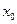 ,使得
,使得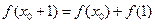 成立.
成立.
(1)试判断函数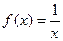 是否属于集合
是否属于集合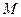 ?请说明理由;
?请说明理由;
(2)设函数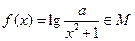 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com