
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由累加法求出an=4+n2-n,$\frac{a_n}{n}$=$\frac{4}{n}$+n-1,利用基本不等式,由此能导出当n=2时$\frac{a_n}{n}$的最小值.
解答 解:an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2[1+2+…+(n-1)]+4=4+n2-n
所以$\frac{a_n}{n}$=$\frac{4}{n}$+n-1
因为$\frac{4}{n}$+n≥4,当且仅当n=2时取等号,
所以当n=2时$\frac{a_n}{n}$的最小值为3.
故选:B.
点评 本题考查了递推数列的通项公式的求解以及基本不等式的运用,考查了同学们综合运用知识解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
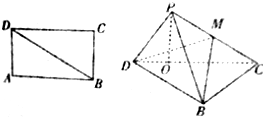 如图,在矩形ABCD中,$AB=6,BC=2\sqrt{3}$,沿对角线BD将三角形ABD向上折起,使点A移至点P,且点P在平面BCD上的射影O在DC上,
如图,在矩形ABCD中,$AB=6,BC=2\sqrt{3}$,沿对角线BD将三角形ABD向上折起,使点A移至点P,且点P在平面BCD上的射影O在DC上,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $λ>-\frac{1}{2}$ | B. | $λ<-\frac{1}{2}$ | C. | λ>-$\frac{1}{2}$且λ≠2 | D. | λ<-$\frac{1}{2}$且λ≠2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com