
在平面直角坐标系 中,已知曲线
中,已知曲线 ,以平面直角坐标系
,以平面直角坐标系 的原点
的原点 为极点,
为极点, 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线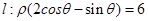 .
.
(1)将曲线 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 、
、 倍后得到曲线
倍后得到曲线 ,试写出直线的直角坐标方程和曲线
,试写出直线的直角坐标方程和曲线 的参数方程;
的参数方程;
(2)在曲线 上求一点
上求一点 ,使点
,使点 到直线的距离最大,并求出此最大值
到直线的距离最大,并求出此最大值
科目:高中数学 来源: 题型:解答题
已知曲线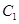 的参数方程是
的参数方程是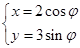 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线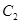 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在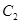 上,且A,B,C,D依逆时针次序排列,点A的极坐标为
上,且A,B,C,D依逆时针次序排列,点A的极坐标为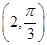 .
.
(Ⅰ)求点A,B,C,D的直角坐标;
(Ⅱ)设P为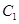 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知P为半圆C: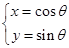 (
(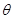 为参数,
为参数,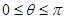 )上的点,点A的坐标为(1,0),
)上的点,点A的坐标为(1,0),
O为坐标原点,点M在射线OP上,线段OM与C的弧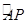 的长度均为
的长度均为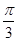 。
。
(Ⅰ)以O为极点, 轴的正半轴为极轴建立极坐标系,求点M的极坐标;
轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(Ⅱ)求直线AM的参数方程。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)(选修4-4:坐标系与参数方程)
在直角坐标系中,直线 的参数方程为
的参数方程为
 为参数).若以坐标原点
为参数).若以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线 的极坐标方程为
的极坐标方程为 .
.
(I)求曲线 的直角坐标方程;
的直角坐标方程;
(II)求直线 被曲线
被曲线 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的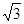 、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
有人收集了春节期间平均气温x与某取暖商品销售额y的有关数据如下表:
| 平均气温(℃) | ﹣2 | ﹣3 | ﹣5 | ﹣6 |
| 销售额(万元) | 20 | 23 | 27 | 30 |
 x+a的系数
x+a的系数 .则预测平均气温为﹣8℃时该商品销售额为( )
.则预测平均气温为﹣8℃时该商品销售额为( )查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是 ( )
A. =-10x+200 =-10x+200 | B. =10x+200 =10x+200 |
C. =-10x-200 =-10x-200 | D. =10x-200 =10x-200 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列结论正确的是( )
①相关关系是一种非确定性关系;
②任一组数据都有回归方程;
③散点图能直观地反映数据的相关程度;
| A.①② | B.②③ | C.①③ | D.①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com