Question

19．设△ABC的内切圆分别切三边BC、CA、AB于D、E、F，X是△ABC内的-点，△XBC的内切圆也在点D处与C相切，并与CX，XB分别切于点Y、Z．证明：EFZY是圆内接四边形．

Answer 1

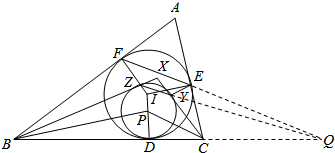
分析 根据已知条件，由切割线定理的逆定理结合梅涅劳斯定理及其逆定理能证明四点共圆，从而能证明EFZY是圆内接四边形．

解答 证明：若EF∥BC，则AB=AC，AD是EFZY的对称轴，
因而四边形EFAY是圆内接四边形；
若EF不平行BC，设EF，BC的延长线交于点P，直线FEP截△ABC，
由梅涅劳斯定理，得：$\frac{AF}{FB}•\frac{BP}{PC}•\frac{CE}{EA}$=1，
又AF=AE，即$\frac{BP}{PC}•\frac{CE}{FB}=1$，
又因为BZ=BD=BF，CY=CD=CE，所以$\frac{BP}{PC}•\frac{CY}{BZ}$=1，
又ZX=XY，即$\frac{XZ}{BZ}•\frac{BP}{PC}•\frac{CY}{YX}=1$，
由梅涅劳斯定理，得Z、Y、P三点共线，
于是PE•PF=PD²=PY•PZ，
由切割线定理的逆定理，得E、F、Z、Y四点共圆．
∴EFZY是圆内接四边形．

点评 本题考查圆内接四边形的证明，是中档题，解题时要注意切割线定理的逆定理、梅涅劳斯定理及其逆定理的合理运用．