

���� ��������Ƶ�ʷֲ�ֱ��ͼ�����ʼ��ɵó���
�������¼�A����δ����ijһ����������̵�������������20�䣻�¼�B����δ����ijһ����������̵�������������20�䣻�¼�C����δ����ijһ����ס����������̵�������ǡ��һ������20������һ��������20�䣮���P��A����P��B����P��C����
����X�Ŀ���ȡֵΪ0��1��2��3�����ö���ֲ��е�����������ʣ��õ��ֲ��У�Ȼ�����������
��� �⣺�����ɸ�С���������Ϊ1��
�ã�0.010+a+0.020+0.025+0.030����10=1��
���a=0.015��
��Ƶ�ʷֲ�ֱ��ͼ�ɿ��������������ȽϷ�ɢ�����ҽ�Ϊ���У���Ҫ������20-30�䣬
��s12��s22��
��II�����¼�A����δ����ijһ����������̵�������������20�䣻
�¼�B����δ����ijһ����������̵�������������20�䣻
�¼�C����δ����ijһ����ס����������̵�������ǡ��һ������20������һ��������20�䣮
��P��A��=0.20+0.10=0.3��P��B��=0.10+0.20=0.3��
��P��C��=P��$\overline{A}$��P��B��+P��A��P��$\overline{B}$��=0.42��
��III���������֪X�����п���ȡֵΪ0��1��2��3��X��B��3��0.3��P��X=k��=${∁}_{3}^{k}��0��{3}^{k}��0��{7}^{3-k}$��
��P��X=0��=0.343��P��X=1��=0.441��P��X=2��=0.189��P��X=3��=0.027��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | 0.343 | 0.441 | 0.189 | 0.027 |
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ�����ʡ�����ֲ��еĸ��ʼ��㹫ʽ��ѧ������������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.1 | B�� | 0.2 | C�� | 0.4 | D�� | 0.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
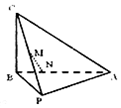 ��ͼ��������C-PAB�У�AB��BC��PB��BC��PA=PB=5��AB=6��BC=4����M��PC���е㣬��N���߶�AB�ϣ���MN��AB��
��ͼ��������C-PAB�У�AB��BC��PB��BC��PA=PB=5��AB=6��BC=4����M��PC���е㣬��N���߶�AB�ϣ���MN��AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
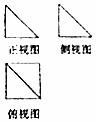 ��ͼ��һ�������������ͼ����������ͼ�Ͳ���ͼ������Ϊ1������ȫ�ȵĵ���ֱ�������Σ���ö�����ĸ����������ij���Ϊ��������
��ͼ��һ�������������ͼ����������ͼ�Ͳ���ͼ������Ϊ1������ȫ�ȵĵ���ֱ�������Σ���ö�����ĸ����������ij���Ϊ��������| A�� | $\sqrt{7}$ | B�� | $\sqrt{5}$ | C�� | 2 | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
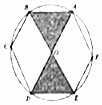 ��֪��������ABCDEF�ڽ���ԲO������AD��BE��������ԲO��Ͷ��2000��С�ף�����Թ���������Ӱ�����ڵ�С�����������ǣ����������ο����ݣ�$\frac{��}{\sqrt{3}}$=1.82��$\frac{\sqrt{3}}{��}$=0.55��
��֪��������ABCDEF�ڽ���ԲO������AD��BE��������ԲO��Ͷ��2000��С�ף�����Թ���������Ӱ�����ڵ�С�����������ǣ����������ο����ݣ�$\frac{��}{\sqrt{3}}$=1.82��$\frac{\sqrt{3}}{��}$=0.55��| A�� | 550 | B�� | 600 | C�� | 650 | D�� | 700 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1] | B�� | ��-�ޣ�-1] | C�� | [-1��+�ޣ� | D�� | [1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ҫ���� | B�� | ��ֲ���Ҫ���� | ||
| C�� | ��Ҫ��������� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com