
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如下折线图.下面关于这位同学的数学成绩的分析中,正确的共有( )个
对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如下折线图.下面关于这位同学的数学成绩的分析中,正确的共有( )个| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
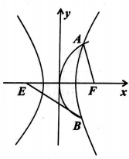 已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )| A. | 4-$\sqrt{7}$ | B. | 4-$\sqrt{3}$ | C. | 4+$\sqrt{3}$ | D. | 4+$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{x}$ | B. | y=-x3 | C. | y=${log_{\frac{1}{2}}}$x | D. | y=x+$\frac{1}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com