
分析 (1)根据$\overrightarrow{a}$⊥$\overrightarrow{b}$.可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,求解出sinα,可得向量$\overrightarrow{a}$,$\overrightarrow{b}$的坐标.即可求|$\overrightarrow{a}$-$\overrightarrow{b}$|;
(2)利用诱导公式化简后,将α带入计算即可.
解答 解:(1)由题意,$\overrightarrow{a}$⊥$\overrightarrow{b}$.
∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,即12-20sinα=0,可得sinα=$\frac{3}{5}$.
∵α∈(0,$\frac{π}{2}$)
∴cosα=$\frac{4}{5}$,
tanα=$\frac{3}{4}$.
∴向量$\overrightarrow{a}$=(4,4),$\overrightarrow{b}$=(3,-3),
那么:$\overrightarrow{a}$-$\overrightarrow{b}$=(1,7)
则|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{1+49}=5\sqrt{2}$
(2)由cos($\frac{3π}{2}$+α)-sin(α-π)=sinα+sinα=2sinα
由(1)可得sinα=$\frac{3}{5}$.
∴cos($\frac{3π}{2}$+α)-sin(α-π)=2sinα=$\frac{6}{5}$.
点评 本题考查了向量的计算和同角三角函数的计算,诱导公式的化解.属于基础题.


科目:高中数学 来源: 题型:解答题
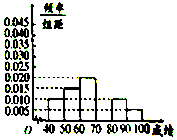 如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题:
如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 体积为18$\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是[8π,16π].
体积为18$\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是[8π,16π].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{π}$ | B. | $\frac{{6\sqrt{3}}}{π}$ | C. | $\frac{4}{3}$ | D. | $\frac{{4\sqrt{3}}}{π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com