练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】△ABC的内角A，B，C所对的边分别为a，b，c．向量 =（a， b）与 =（cosA，sinB）平行．
    （Ⅰ）求A；
    （Ⅱ）若a= ，b=2，求△ABC的面积．

    【答案】解：（Ⅰ）因为向量 =（a， b）与 =（cosA，sinB）平行，

    所以asinB﹣ =0，由正弦定理可知：sinAsinB﹣ sinBcosA=0，因为sinB≠0，

    所以tanA= ，可得A= ；

    （Ⅱ）a= ，b=2，由余弦定理可得：a2=b2+c2﹣2bccosA，可得7=4+c2﹣2c，解得c=3，

    △ABC的面积为： = ．


    【解析】（I）先由与平行可得asinB- bcosA=0，再利用正弦定理将边转化为角，可得tanA，进而可得A； （II）先利用余弦定理可得c，再利用三角形的面积公式可得△ABC的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2015年一交警统计了某路段过往车辆的车速大小与发生的交通事故次数,得到如下表所示的数据:

    车速x(km/h)

    60

    70

    80

    90

    100

    事故次数y

    1

    3

    6

    9

    11

    (Ⅰ)请画出上表数据的散点图;

    (Ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程=x+;

    (Ⅲ)试根据(Ⅱ)求出的线性回归方程,预测在2016年该路段路况及相关安全设施等不变的情况下,车速达到110km/h时,可能发生的交通事故次数.

    (附:b=,=-,其中,为样本平均值)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某班级举行一次知识竞赛活动，活动分为初赛和决赛两个阶段、现将初赛答卷成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．

    分数（分数段）

    频数（人数）

    频率

    [60，70）

    ①

    0.16

    [70，80）

    22

    ②

    [80，90）

    14

    0.28

    [90，100）

    ③

    ④

    合计

    50

    1


    （1）填充频率分布表中的空格（在解答中直接写出对应空格序号的答案）；
    （2）决赛规则如下：参加决赛的每位同学依次口答4道小题，答对2道题就终止答题，并获得一等奖．如果前三道题都答错，就不再答第四题．某同学进入决赛，每道题答对的概率P的值恰好与频率分布表中不少于80分的频率的值相同．
    ①求该同学恰好答满4道题而获得一等奖的概率；
    ②记该同学决赛中答题个数为X，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正四棱锥P﹣ABCD中，AB=2，PA= ，E是棱PC的中点，过AE作平面分别与棱PB、PD交于M、N两点．
    （1）若PM= PB，PN=λPD，求λ的值；
    （2）求直线PA与平面AMEN所成角的正弦值的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若点O在内，且满足，设为的面积， 为的面积，则＝________.

    【答案】

    【解析】由，可得：

    延长OA，OB，OC，使OD=2OA，OE=4OB，OF=3OC，

    如图所示：

    ∵2+3+4=，

    ∴，

    即O是△DEF的重心，

    故△DOE，△EOF，△DOF的面积相等，

    不妨令它们的面积均为1，

    则△AOB的面积为，△BOC的面积为，△AOC的面积为，

    故三角形△AOB，△BOC，△AOC的面积之比依次为： ： ： =3：2：4，

    .

    故答案为： ．

    点睛：本题考查的知识点是三角形面积公式，三角形重心的性质，平面向量在几何中的应用，注意重要结论：点O在内，且满足， 则三角形△AOB，△BOC，△AOC的面积之比依次为： .

    【题型】填空题
    【结束】
    16

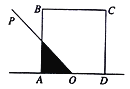
    【题目】如图，正方形ABCD的边长为2，O为AD的中点，射线OP从OA出发，绕着点O顺时针方向旋转至OD，在旋转的过程中，记为OP所经过的在正方形ABCD内的区域（阴影部分）的面积，那么对于函数有以下三个结论：

    ①；

    ②任意，都有；

    ③任意且，都有.

    其中正确结论的序号是__________. （把所有正确结论的序号都填上）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《九章算术》是我国古代数学经典名著，它在集合学中的研究比西方早1千年，在《九章算术》中，将四个面均为直角三角形的四面体称为鳖臑，已知某“鳖臑”的三视图如图所示，则该鳖臑的外接球的表面积为（ ）
    A.200π
    B.50π
    C.100π
    D. π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为2，O为AD的中点，射线OP从OA出发，绕着点O顺时针方向旋转至OD，在旋转的过程中，记为OP所经过的在正方形ABCD内的区域（阴影部分）的面积，那么对于函数有以下三个结论：

    ①；

    ②任意，都有；

    ③任意且，都有.

    其中正确结论的序号是__________. （把所有正确结论的序号都填上）.

    【答案】①②

    【解析】试题分析：①：如图，当时， 与相交于点，∵，则，

    ∴，∴①正确；②：由于对称性， 恰好是正方形的面积，

    ∴，∴②正确；③：显然是增函数，∴，∴③错误．

    考点：函数性质的运用．

    【题型】填空题
    【结束】
    17

    【题目】化简

    （1）

    （2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： （a＞b＞0）左、右焦点分别为F1 ， F2 ， A（2，0）是椭圆的右顶点，过F2且垂直于x轴的直线交椭圆于P，Q两点，且|PQ|=3；
    （1）求椭圆的方程；
    （2）若直线l与椭圆交于两点M，N（M，N不同于点A），若 =0， = ；
    ①求证：直线l过定点；并求出定点坐标；
    ②求直线AT的斜率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 （ ）的最大值为 ，最小值为 .

    （1）求 的值；

    （2）将函数 图象向右平移 个单位后，再将图象上所有点的纵坐标扩大到原来的 倍，横坐标不变，得到函数 的图象，求方程 的解.

    查看答案和解析>>

    同步练习册答案