
分析 (I)根据an+1=Sn+1-Sn可得出{an}是等比数列,根据等差中项的定义列方程可求出公比q,从而得出{an}的通项公式;
(II)求出bn,令bn+1-bn>0可得λ<$\frac{{2}^{n}}{2n+1}$恒成立,求出右侧数列的最小值即可得出λ的范围.
解答 解:(I)∵Sn+1=qSn+1,∴当n≥2时,Sn=qSn-1+1,
∴an+1=Sn+1-Sn=qSn-qSn-1=qan,
又S2=qS1+1,a1=S1=1,
∴a2=q=qa1,
∴数列{an}是首项为1,公比为1的等比数列,
∵2a2,a3,a2+2成等差数列,
∴2a3=2a2+a2+2=3a2+2,
即2q2=3q+2,解得q=2或q=-$\frac{1}{2}$(舍).
∴an=2n-1.
(II)bn=2n-λn2,
∴bn+1-bn=2n+1-λ(n+1)2-2n+λn2=2n-2nλ-λ,
∵数列{bn}为递增数列,
∴2n-2nλ-λ>0恒成立,即λ<$\frac{{2}^{n}}{2n+1}$恒成立,
令cn=$\frac{{2}^{n}}{2n+1}$,则cn+1-cn=$\frac{{2}^{n+1}}{2n+3}$-$\frac{{2}^{n}}{2n+1}$=2n($\frac{2}{2n+3}-\frac{1}{2n+1}$)=2n$\frac{2n-1}{(2n+3)(2n+1)}$>0,
∴{cn}是递增数列,
∴cn≥c1=$\frac{2}{3}$,
∴λ<$\frac{2}{3}$.
点评 本题考查了等比数列的性质,数列单调性的判断,属于中档题.


科目:高中数学 来源: 题型:解答题
| 赠送话费(单位:元) | 10 | 20 |
| 概率 | $\frac{2}{3}$ | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<3} | B. | {x|x≤-2} | C. | {x|x<-2} | D. | {x|x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
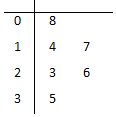 据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级.某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级.某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
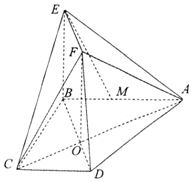 如图所示,直角梯形ABCD两条对角线AC,BD的交点为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,M为线段AB上一点,AM=2MB,且AB⊥BC,AB∥CD,AB=BE=6,CD=BC=3.
如图所示,直角梯形ABCD两条对角线AC,BD的交点为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,M为线段AB上一点,AM=2MB,且AB⊥BC,AB∥CD,AB=BE=6,CD=BC=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com