
分析 (Ⅰ)求出双曲线的顶点,可得抛物线的焦点,进而得到抛物线方程;
(Ⅱ)假设存在实数m,使得直线x=m总是与圆C相切,由直线和圆相切的条件:d=r,结合抛物线的定义,可得AB的长,进而得到m=-1总成立,即可判断存在.
解答 解:(Ⅰ)双曲线x2-y2=1的右顶点为(1,0),
则抛物线的焦点为(1,0),
即有抛物线Г的标准方程为y2=4x;
(Ⅱ)假设存在实数m,使得直线x=m总是与圆C相切,
即有圆心到直线的距离等于AB长的一半.
抛物线的准线为x=-1,
设AB的中点为D,由于直线AB经过焦点(1,0),
设A(x1,y1),B(x2,y2),
则由抛物线的定义可得,|AB|=x1+1+x2+1=(x1+x2)+2,
由假设可得|$\frac{{x}_{1}+{x}_{2}}{2}$-m|=1+$\frac{{x}_{1}+{x}_{2}}{2}$,
即有m=-1,
故存在实数m=-1,使得直线x=-1总是与圆C相切.
点评 本题考查抛物线的方程和性质,主要考查抛物线的定义和方程的运用,同时考查直线和圆的位置关系:相切,属于中档题.


科目:高中数学 来源: 题型:解答题
 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和
如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和查看答案和解析>>
科目:高中数学 来源: 题型:解答题
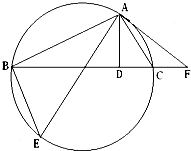 如图,AD是△ABC的高,AE是△ABC的外接圆的直径,过点A作圆的切线交BC的延长线于点F.
如图,AD是△ABC的高,AE是△ABC的外接圆的直径,过点A作圆的切线交BC的延长线于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | θn随着n的增大而增大 | B. | θn随着n的增大而减小 | ||
| C. | 随着n的增大,θn先增大后减小 | D. | 随着n的增大,θn先减小后增大 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com