
|
| Sn-tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
| 8(1-8n) |
| 1-8 |
| 8 |
| 7 |
| Sn-tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
(
| ||||
(
|
| 1 |
| 2 |
| ||||
|
| 1 |
| 2 |
| 8n |
| 7 |
| 15 |
| 7 |
| 8 |
| 7 |
| 1 |
| 7 |
| 8 |
| 7 |
| 15 |
| 7 |
| Sn-tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
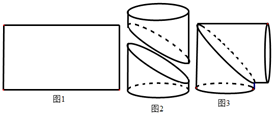 工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是( )
工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是( )| A、一段圆弧 |
| B、一段抛物线 |
| C、一段双曲线 |
| D、一段正弦曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、f(sinA)≤f(cosB) |
| B、f(sinA)≥f(cosB) |
| C、f(sinA)≤f(sinB) |
| D、f(cosA)≤f(cosB) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 1 |
| 3 |
| 5 |
| 5 |
| 1 |
| 5 |
| 7 |
| 7 |
| 1 |
| 7 |
| 9 |
| 9 |
| 1 |
| 9 |
| 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| OM |
| ON |
| PM |
| PN |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com