
分析 (1)根据抛物线的定义结合圆的性质建立方程关系进行求解即可.
(2)根据抛物线与圆的位置关系求出圆心T的坐标,结合直线和圆的位置关系进行求解即可.
解答 (1)∵y2=2px(p>0)上一点P到其焦点F的距离为$\frac{3}{2}$,
∴|PF|=$\frac{3}{2}$,
∵以P为原点且与抛物线准线l相切的圆恰好过原点O,
∴|PO|=|PF|=$\frac{3}{2}$,
即△POF为等腰三角形,过P作PQ⊥x于Q,
则x=$\frac{p}{4}$,
∴$\frac{p}{2}+\frac{p}{4}=\frac{3}{2}$得p=2,
∴抛物线的方程为y2=4x.
(2)设T(x0,y0),圆C2的半径为r,
∵T是抛物线y2=4x上的动点,
∴.y02=4x0,(x0≥0),
∴|AT|=$\sqrt{({x}_{0}-a)^{2}+({y}_{0}-0)^{2}}$=$\sqrt{[{x}_{0}-(a-2)]^{2}+4a-4}$,
∵a>2,∴a-2>0,
则当x0=a-2时,AT取得最小值为2$\sqrt{a-1}$,
由2$\sqrt{a-1}$=a-1,平方得a2-6a+5=0,得a=5或a=1(舍),
则当x0=a-2=3,y02=4x0=12,即y0=±2$\sqrt{3}$,
∴圆C2的圆心T(3,±2$\sqrt{3}$),
∵圆C2与y轴交于M,N两点,且|MN|=4,
∴|MN|=2$\sqrt{{r}^{2}-{{x}_{0}}^{2}}$=4,
∴r=$\sqrt{4+{{x}_{0}}^{2}}$=$\sqrt{13}$,
∵点T到直线l的距离d=|x0+1|=4$>\sqrt{13}$,
∴直线l与圆C2相离.
点评 本题主要考查抛物线方程的求解,以及直线和圆的位置关系的判断,综合性考查圆锥曲线的性质,运算量量较大,综合性较强.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
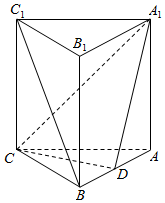 已知:三棱柱ABC-A1B1C1中,A1A⊥平面ABC,CA=CB,D是AB的中点,E是B1C1中点
已知:三棱柱ABC-A1B1C1中,A1A⊥平面ABC,CA=CB,D是AB的中点,E是B1C1中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com