练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    直三棱柱ABC－A′B′C′中，AC＝BC＝AA′，∠ACB＝90°，D、E分别为AB、BB′的中点．

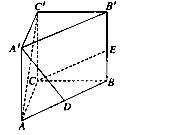
     (1)求证：CE⊥A′D；

    (2)求异面直线CE与AC′所成角的余弦值．



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设P < 0 是一常数,过点`Q(2P,0)的直线与抛物线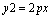交于相导两点A、B 以线段AB 为直径作圆H(H为圆心).试证抛物线顶点在圆H的圆周上;并求圆H的面积最小时直线AB的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°E、F分别是AC、AD上的动点，且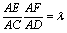（0<λ<1），如图。

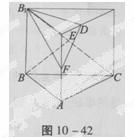
    （1）求证：不论λ为何值，恒有平面BEF⊥平面ABC；

    （2）当λ为何值时，平面BEF⊥平面ACD。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     矩形ABCD的两边AB=3，AD=4，PA⊥平面ABCD，且PA=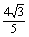，则二面角A-BD-P的度数为  （  ）

    A．30°         B．45°        C．60°           D．75°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正方体ABCD－A1B1C1D1的棱长为a，点M在AC1上且＝，N为B1B的中点，则||为(　　)

    A.a                B.a

    C.a                D.a

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，AC是圆O的直径，点B在圆O上，∠BAC＝30°，BM⊥AC交AC于点M，EA⊥平面ABC，FC∥EA，AC＝4，EA＝3，FC＝1.

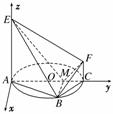
     (1)证明：EM⊥BF；

    (2)求平面BEF与平面ABC所成的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某电器商经过多年经验发现本店每个月售出的电冰箱的台数ξ是一个随机变量，它的分布列如下：

    ξ

    1

    2

    3

    …

    12

    P

    …

    设每售出一台电冰箱，电器商获利300元，如销售不出而囤积于仓库，则每台每月需花保养费100元，问电器商月初购进多少台电冰箱才能使自己平均收益最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设不等式组表示的平面区域为D，在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图：一个质点在第一象限运动，在第一秒钟内它由原点运动到(0,1)，而后接着按图所示在与x轴，y轴平行的方向上运动，且每秒移动一个单位长度，那么2 000秒后，这个质点所处位置的坐标是(　　)

    A．(44,25)    B．(45,25)     C．(25,45)    D．(24,44)

    查看答案和解析>>

    同步练习册答案