练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     矩形ABCD的两边AB=3，AD=4，PA⊥平面ABCD，且PA=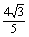，则二面角A-BD-P的度数为  （  ）

    A．30°         B．45°        C．60°           D．75°


    A


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知点P(x,y)在不等式组  

    A．[-2，-1]          B.[-2,1]

    C.[-1,2]             D.[1,2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图10-11，四棱锥P—ABCD的底面是正方形，PA⊥底面ABCD，AE⊥PD，EF∥CD，AM=EF。

     

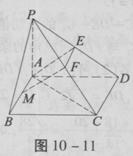
    （1）证明MF是异面直线AB与PC的公垂线；

     （2）若PA=3AB，求直线AC与平面EAM所成角的正弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图11-1，四棱锥P—ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=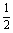AB=1，M是PB的中点。

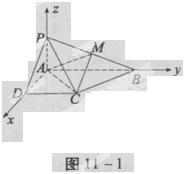
    （1）证明：面PAD⊥面PCD；

    （2）求AC与PB所成的角；

    （3）求面AMC与面BMC所成二面角A-CM-B的大小。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图11-2，在直四棱术ABCD-A1B1C1D1中，AB=AD=2，DC=2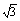，AA1=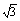，AD⊥DC，AC⊥BD，垂足为E。

    （1）求证BD⊥A1C；

    （2）求二面角A1-BD-C1的大小；

    （3）求异面直线AD与BC1所成角的大小。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设空间四点O，A，B，P满足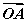＝＋t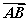，其中0<t<1，则有(　　)

    A．点P在线段AB上

    B．点P在线段AB的延长线上

    C．点P在线段BA的延长线上

    D．点P不一定在直线AB上

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直三棱柱ABC－A′B′C′中，AC＝BC＝AA′，∠ACB＝90°，D、E分别为AB、BB′的中点．

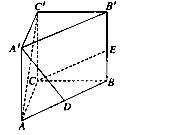
     (1)求证：CE⊥A′D；

    (2)求异面直线CE与AC′所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲、乙两人各射击一次，击中目标的概率分别是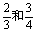。假设两人射击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响。

    （1）求甲射击4次，至少1次未击中目标的概率；

    （2）求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；

    （3）假设某人连续2次未击中目标，则停止射击。问：乙恰好射击5次后，被中止射击的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)， 第3组[85，90)，第4组[90，95)，第5组[95，100]得到的频率分布直方图如图所示．

    （I）分别求第3，4，5组的频率；

    （Ⅱ） 若该校决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，

    (ⅰ) 已知学生甲和学生乙的成绩均在第三组，求学生甲和学生乙同时进入第二轮面试的概率；

    (ⅱ) 学校决定在这6名学生中随机抽取2名学生接受考官D的面试，设第4组中有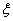名学生被考官D面试，求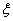的分布列和数学期望.

    查看答案和解析>>

    同步练习册答案