练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图10-11，四棱锥P—ABCD的底面是正方形，PA⊥底面ABCD，AE⊥PD，EF∥CD，AM=EF。

     

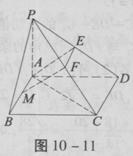
    （1）证明MF是异面直线AB与PC的公垂线；

     （2）若PA=3AB，求直线AC与平面EAM所成角的正弦值。


    （2）解法一：连接BD交AC于O，连接BE，过O作OH⊥BE，H为垂足，∵AE⊥PD，CD⊥PD，EF∥CD，∴EF⊥PD，PD⊥平面MAE，又OH⊥BE，∴OH∥DE，∴OH⊥平面MAE。连接AH，则∠HAO是直线AC与平面MAE所成的角，设AB=a则PA=3a，AO=AC=，因Rt△ADE~Rt△PDA,故ED=从而Rt△AHO中，sin∠HAO=

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    （）=   （  ）

    A．-         B．        C．-        D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设P < 0 是一常数,过点`Q(2P,0)的直线与抛物线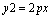交于相导两点A、B 以线段AB 为直径作圆H(H为圆心).试证抛物线顶点在圆H的圆周上;并求圆H的面积最小时直线AB的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    .已知直线与双曲线的一条渐近线平行，则这两条平行直线之间的距离是                                                     。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在长方体ABCD—A1B1C1D1中，已知AB=4，AD=3，AA1=2，E、F分别是线段AB、BC上的点，且EB=FB=1。

     （1）求二面角C—DE—C1的正切值

     （2）求直线EC1与FD1所成角的余弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正方体ABCDA1B1C1D1中，E，F分别为棱AA1，CC1的中点，则在空间中与三条直线A1D1，EF，CD都相交的直线（    ）

    A．不存在        B．有且只有两条    C．有且只有三条 D．有无数条

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°E、F分别是AC、AD上的动点，且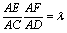（0<λ<1），如图。

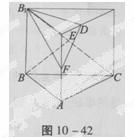
    （1）求证：不论λ为何值，恒有平面BEF⊥平面ABC；

    （2）当λ为何值时，平面BEF⊥平面ACD。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     矩形ABCD的两边AB=3，AD=4，PA⊥平面ABCD，且PA=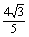，则二面角A-BD-P的度数为  （  ）

    A．30°         B．45°        C．60°           D．75°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设不等式组表示的平面区域为D，在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率是________．

    查看答案和解析>>

    同步练习册答案