
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
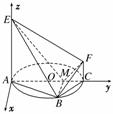
(1)证明:EM⊥BF;
(2)求平面BEF与平面ABC所成的锐二面角的余弦值.
科目:高中数学 来源: 题型:
如图11-1,四棱锥P—ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=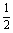 AB=1,M是PB的中点。
AB=1,M是PB的中点。
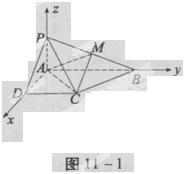
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角A-CM-B的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
设空间四点O,A,B,P满足 =
=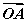 +t
+t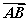 ,其中0<t<1,则有( )
,其中0<t<1,则有( )
A.点P在线段AB上
B.点P在线段AB的延长线上
C.点P在线段BA的延长线上
D.点P不一定在直线AB上
查看答案和解析>>
科目:高中数学 来源: 题型:
直三棱柱ABC-A′B′C′中,AC=BC=AA′,∠ACB=90°,D、E分别为AB、BB′的中点.
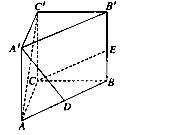
(1)求证:CE⊥A′D;
(2)求异面直线CE与AC′所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
盒子中有大小相同的球10个,其中标号为1的球3个,标号为2的球4个,标号为5的球3个。第一次从盒子中任取1个球,放回后第二次再任取1个球(假设取到每个球的可能性都相同)。记第一次与第二次取得球的标号之和 为ξ。
为ξ。
(1)求随机变量ξ的分布列;
(2)求随机变量ξ的期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两人各射击一次,击中目标的概率分别是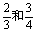 。假设两人射击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
。假设两人射击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击。问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
盒子中装有形 状、大小完全相同的3个红球和2个白球,从中随机取出一个记下颜色后放回,当红球取到2次时停止取球.那
状、大小完全相同的3个红球和2个白球,从中随机取出一个记下颜色后放回,当红球取到2次时停止取球.那 么取球次数恰为3次的概率是( )
么取球次数恰为3次的概率是( )
A. 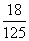 B.
B. 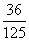 C.
C. 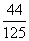
 D.
D. 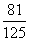
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com