
分析 (1)求出y的解析式,利用绝对值不等式即可求解a的值.
(2)函数含有绝对值,即可考虑到分类讨论去掉绝对值号,分别讨论当x=-4时,当x>-4时,当x<-4的情况,可得不同解析式求解不等式即可.
解答 解:(1)由题意,函数f(x)=|x+4|.
那么y=f(2x+a)+f(2x-a)=|2x+a+4|+|2x-a+4|≥|2x+a-4-(2x-a+4)|=|2a|
∵最小值为4,即|2a|=3,
∴a=$±\frac{3}{2}$
(2)函数f(x)=|x+4|=$\left\{\begin{array}{l}{x+4,(x>-4)}\\{0,(x=-4)}\\{-4-x,(x<-4)}\end{array}\right.$
∴不等式f(x)>1-$\frac{1}{2}$x等价于$\left\{\begin{array}{l}{x+4>1-\frac{1}{2}x,(x>-4)}\\{-4-x>1-\frac{1}{2}x,(x<-4)}\end{array}\right.$,解得:x>-2或x<-10
故得不等式f(x)>1-$\frac{1}{2}$x的解集为{x|x>-2或x<-10}.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,属于基础题


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{9}$ | B. | -9 | C. | $\frac{1}{9}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
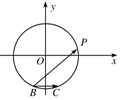 已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )
已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com