
| A�� | $\frac{��}{6}$��A��$\frac{5��}{6}$ | B�� | $\frac{��}{6}$��A$��\frac{��}{2}$ | C�� | $\frac{��}{6}$��B$��\frac{5��}{6}$ | D�� | $\frac{��}{6}$��B$��\frac{��}{2}$ |
���� �����ƽ�����������ļ������壬��|$\overrightarrow{AB}$-t$\overrightarrow{AC}$|��$\frac{1}{2}$|$\overrightarrow{AB}$|������t������|���Ӷ��ó���A�Ĵ�С��
��� �⣺��ABC�У��������t������|$\overrightarrow{AB}$-t$\overrightarrow{AC}$|��$\frac{1}{2}$|$\overrightarrow{AB}$|������
����ȡt=1����|$\overrightarrow{AB}$-$\overrightarrow{AC}$|��$\frac{1}{2}$|$\overrightarrow{AB}$|������
��|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=|$\overrightarrow{CB}$|��$\frac{1}{2}$|$\overrightarrow{AB}$|��
��cosA=$\frac{{AB}^{2}{+AC}^{2}{-BC}^{2}}{2AB•AC}$��$\frac{{\frac{3}{4}AB}^{2}{+AC}^{2}}{2AB•AC}$
��$\frac{3}{4}$AB2+AC2��2•$\frac{\sqrt{3}}{2}$AB•AC
��cosA��$\frac{\sqrt{3}}{2}$��
��cosA��-$\frac{1}{2}$��
��$\frac{��}{6}$��A��$\frac{5��}{6}$��
��ѡ��A��
���� ���⿼����ƽ�������������������⣬����Ĺؼ���ת������|$\overrightarrow{AB}$-t$\overrightarrow{AC}$|��$\frac{1}{2}$|$\overrightarrow{AB}$|�������⣮


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2\sqrt{m-1}}{m-1}$ | B�� | $\frac{-2\sqrt{-m}}{m}$ | C�� | $\frac{2\sqrt{m}}{m}$ | D�� | -$\frac{2\sqrt{1-m}}{m-1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
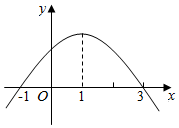 ��f�䣨x���Ǻ���f��x���ĵ�������y=f�䣨x���IJ���ͼ����ͼ��ʾ����y=f ��x����ͼ�����п�����ͼ�еģ�������
��f�䣨x���Ǻ���f��x���ĵ�������y=f�䣨x���IJ���ͼ����ͼ��ʾ����y=f ��x����ͼ�����п�����ͼ�еģ�������| A�� |  | B�� |  | ||
| C�� | 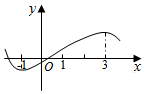 | D�� | 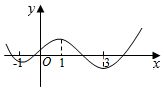 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪˫����C1����ԲC2����ͬ�Ľ���F1��-c��0����F2��c��0����c��0�����������ڵ�һ�����ڵĽ���ΪP����ԲC2��y�Ḻ����ΪB����P��F2��B���㹲�ߣ�F2��$\overrightarrow{PB}$���ɵı�Ϊ1��2����ֱ��PB��˫����C1����һ������ΪQ����|F2Q|=$\frac{\sqrt{3}}{5}$����˫����C1����ԲC2�ķ��̣�
��֪˫����C1����ԲC2����ͬ�Ľ���F1��-c��0����F2��c��0����c��0�����������ڵ�һ�����ڵĽ���ΪP����ԲC2��y�Ḻ����ΪB����P��F2��B���㹲�ߣ�F2��$\overrightarrow{PB}$���ɵı�Ϊ1��2����ֱ��PB��˫����C1����һ������ΪQ����|F2Q|=$\frac{\sqrt{3}}{5}$����˫����C1����ԲC2�ķ��̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com