
分析 构造辅助函数F(x)=$\frac{f(x)}{{e}^{x}}$,求导,由已知条件可知F(x)在定义域R上单调递增,将原不等式转化成$\frac{f(x)}{{e}^{x}}$>$\frac{f(1)}{e}$,根据单调即可求得x的取值范围.
解答 解:设F(x)=$\frac{f(x)}{{e}^{x}}$,
F′(x)=$\frac{f′(x){e}^{x}-{e}^{x}f(x)}{{e}^{2x}}$=$\frac{f′(x)-f(x)}{{e}^{x}}$>0,
∴F(x)在定义域R上单调递增,
将原不等式f(x)>ex-1f(1),
转化成$\frac{f(x)}{{e}^{x}}$>$\frac{f(1)}{e}$,即F(x)>F(1),
∴x>1,
故答案为:(1,+∞).
点评 本题考查导数的运用:求单调性,考查函数的单调性的运用:解不等式,同时考查构造函数,判断单调性,属于中档题.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
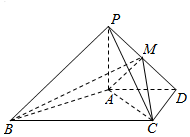 如图.在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ADC=90°,且PA=2,AD=CD=$\frac{1}{2}$BC=2$\sqrt{2}$,点M在PD上.
如图.在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ADC=90°,且PA=2,AD=CD=$\frac{1}{2}$BC=2$\sqrt{2}$,点M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知多面体ABCDEFG是由一个平面截长方体ABCD-A1B1C1D1所得的几何体,如图所示,其中AB=2BC=2AF=4CG=4.
已知多面体ABCDEFG是由一个平面截长方体ABCD-A1B1C1D1所得的几何体,如图所示,其中AB=2BC=2AF=4CG=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com