Question

9．向面积为S的平行四边形ABCD内任投一点M，则△MCD的面积小于$\frac{S}{3}$的概率为$\frac{2}{3}$．

Answer 1

分析 先求出△MCD的面积等于$\frac{S}{3}$时，对应的位置，然后根据几何概型的概率公式求相应的面积，即可得到结论．

解答 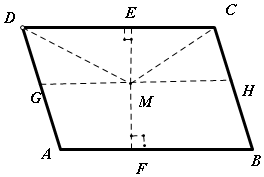解：设△MCD的高为ME，ME的反向延长线交AB于F，当“△MCD的面积等于$\frac{S}{3}$”时，即ME=$\frac{2}{3}$EF，
过M作GH∥AB，如图，则满足△MCD的面积小于$\frac{S}{3}$的点在?CDGH中，由几何概型的公式得到△MCD的面积小于$\frac{S}{3}$的概率为 $\frac{\frac{2S}{3}}{S}=\frac{2}{3}$；
故答案为：$\frac{2}{3}$．

点评 本题主要考查几何概型的概率概率的计算，选择面积之比是解决本题的关键．