
Ζ÷Έω Ά®ΙΐœρΝΩ$\overrightarrow{a}$Θ§$\overrightarrow{b}$Θ§$\overrightarrow{c}$ΙΙ≥…»ΐΫ«–ΈΘ§άϊ”ΟΓœBAC=60ΓψΘ§ΓœABC=45ΓψΘ§ΦΤΥψΫχΕχΦ¥ΒΟΫα¬έΘ°
Ϋβ¥π 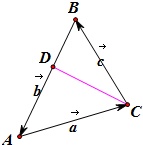 ΫβΘΚΓΏœρΝΩ$\overrightarrow{a}$Θ§$\overrightarrow{b}$Θ§$\overrightarrow{c}$¬ζΉψ$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$Θ§
ΫβΘΚΓΏœρΝΩ$\overrightarrow{a}$Θ§$\overrightarrow{b}$Θ§$\overrightarrow{c}$¬ζΉψ$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$Θ§
ΓύœρΝΩ$\overrightarrow{a}$Θ§$\overrightarrow{b}$Θ§$\overrightarrow{c}$ΡήΙΙ≥…»ΐΫ«–ΈΘ§
ΓΏ$\overrightarrow{a}$”κ$\overrightarrow{b}$ΒΡΦ–Ϋ«Β»”Ύ120ΓψΘ§$\overrightarrow{b}$”κ$\overrightarrow{c}$ΒΡΦ–Ϋ«Β»”Ύ135ΓψΘ§
ΓύΓœBAC=180Γψ-120Γψ=60ΓψΘ§ΓœABC=180Γψ-135Γψ=45ΓψΘ§
ΙΐΒψCΒΫAB±Ώ¥ΙœΏCDΫΜAB”ΎDΘ§
ΓΏBC=|$\overrightarrow{c}$|=3Θ§ΓύCD=BCsinΓœABC=3sin45Γψ=$\frac{3\sqrt{2}}{2}$Θ§
”÷ΓΏCD=ACsinΓœBAC=ACsin60Γψ=$\frac{\sqrt{3}}{2}$ACΘ§
Γύ$\frac{\sqrt{3}}{2}$AC=$\frac{3\sqrt{2}}{2}$Θ§
ΓύAC=$\sqrt{6}$Θ§Φ¥|$\overrightarrow{a}$|=$\sqrt{6}$Θ§
Ι ¥πΑΗΈΣΘΚ$\sqrt{6}$Θ°
ΒψΤά ±ΨΧβΩΦ≤ι«σœρΝΩΒΡΡΘΘ§άϊ”Ο$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$ΙΙΫ®»ΐΫ«–Έ «ΫβΨω±ΨΧβΒΡΙΊΦϋΘ§ΉΔ“βΫβΧβΖΫΖ®ΒΡΜΐάέΘ§ τ”Ύ÷–ΒΒΧβΘ°


 »Ϊ”≈ΩΦΒδΒΞ‘ΣΦλ≤βΨμΦΑΙιάύΉήΗ¥œΑœΒΝ–¥πΑΗ
»Ϊ”≈ΩΦΒδΒΞ‘ΣΦλ≤βΨμΦΑΙιάύΉήΗ¥œΑœΒΝ–¥πΑΗ ΤΖ―ßΥΪ”≈ΨμœΒΝ–¥πΑΗ
ΤΖ―ßΥΪ”≈ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ

| AΘ° | $\frac{{\sqrt{3}}}{3}c{m^3}$ | BΘ° | $\frac{{4\sqrt{3}}}{3}c{m^3}$ | CΘ° | $\frac{{8\sqrt{3}}}{3}c{m^3}$ | DΘ° | $\sqrt{3}c{m^3}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
 »ΐάβΉΕΒΡ»ΐ ”ΆΦ»γΆΦΥυ ΨΘ§‘ρΗΟ»ΐάβΉΕΒΡΧεΜΐΈΣ$\frac{{2\sqrt{3}}}{3}$Θ°
»ΐάβΉΕΒΡ»ΐ ”ΆΦ»γΆΦΥυ ΨΘ§‘ρΗΟ»ΐάβΉΕΒΡΧεΜΐΈΣ$\frac{{2\sqrt{3}}}{3}$Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | y=$\sqrt{{x}^{2}}$”κy=x | BΘ° | y=x0”κy=1 | ||
| CΘ° | y=2${\;}^{lo{g}_{4}x}$”κy=$\frac{x}{\sqrt{x}}$ | DΘ° | y=x”κy=Θ®$\sqrt{x}Θ©^{2}$2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
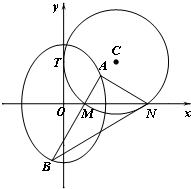 »γΆΦΘ§‘≤C”κy÷αœύ«–”ΎΒψTΘ®0Θ§2Θ©Θ§”κx÷α’ΐΑκ÷αœύΫΜ”ΎΝΫΒψMΓΔNΘ®ΒψM‘ΎΒψNΒΡΉσ≤ύΘ©Θ§«“|MN|=3Θ°
»γΆΦΘ§‘≤C”κy÷αœύ«–”ΎΒψTΘ®0Θ§2Θ©Θ§”κx÷α’ΐΑκ÷αœύΫΜ”ΎΝΫΒψMΓΔNΘ®ΒψM‘ΎΒψNΒΡΉσ≤ύΘ©Θ§«“|MN|=3Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com